Page 228

9-4 Vol. 1

PROGRAMMING WITH INTEL® MMX™ TECHNOLOGY

9.2.5

Single Instruction, Multiple Data (SIMD) Execution Model

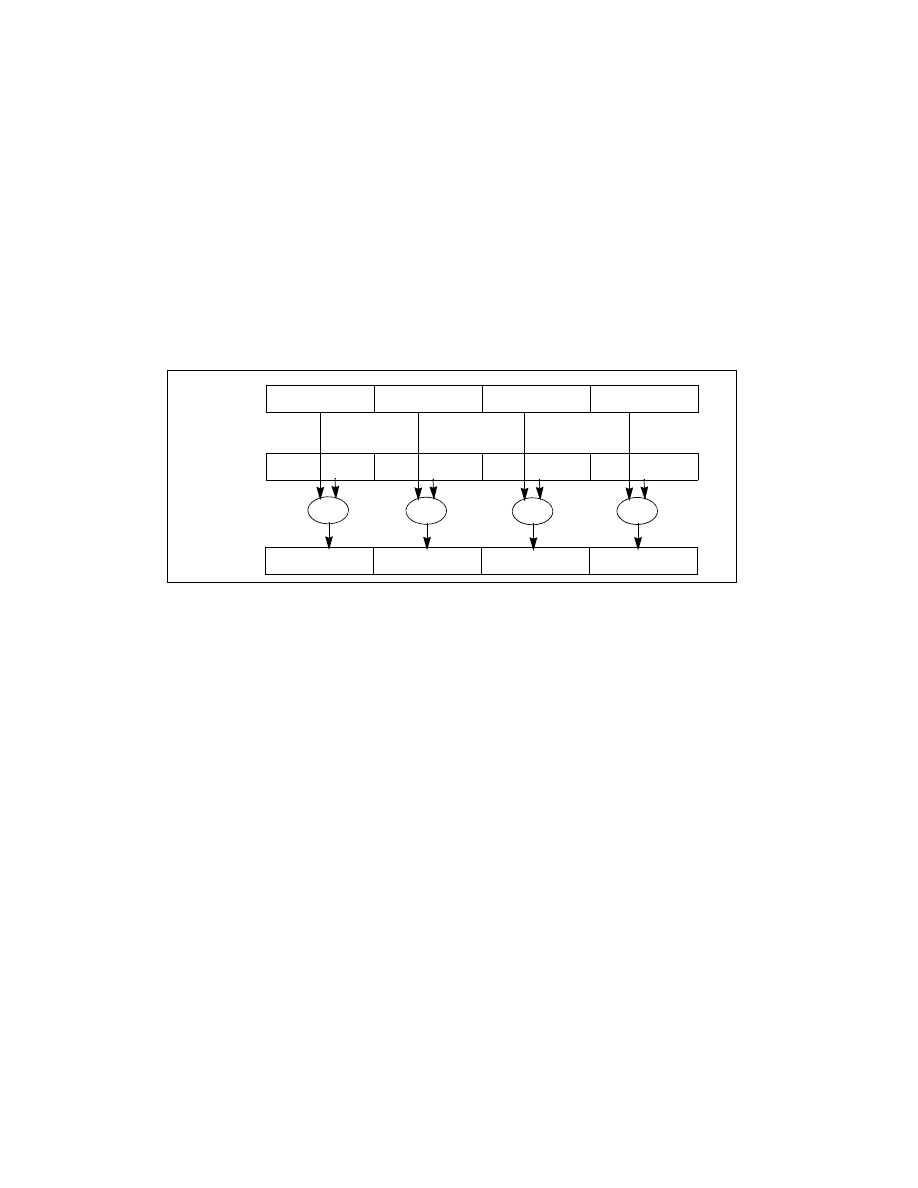
MMX technology uses the single instruction, multiple data (SIMD) technique for performing arithmetic and logical
operations on bytes, words, or doublewords packed into MMX registers (see Figure 9-4). For example, the PADDSW
instruction adds 4 signed word integers from one source operand to 4 signed word integers in a second source
operand and stores 4 word integer results in a destination operand. This SIMD technique speeds up software
performance by allowing the same operation to be carried out on multiple data elements in parallel. MMX tech-
nology supports parallel operations on byte, word, and doubleword data elements when contained in MMX regis-
ters.
The SIMD execution model supported in the MMX technology directly addresses the needs of modern media,
communications, and graphics applications, which often use sophisticated algorithms that perform the same oper-
ations on a large number of small data types (bytes, words, and doublewords). For example, most audio data is
represented in 16-bit (word) quantities. The MMX instructions can operate on 4 words simultaneously with one
instruction. Video and graphics information is commonly represented as palletized 8-bit (byte) quantities. In
Figure 9-4, one MMX instruction operates on 8 bytes simultaneously.

9.3

SATURATION AND WRAPAROUND MODES

When performing integer arithmetic, an operation may result in an out-of-range condition, where the true result
cannot be represented in the destination format. For example, when performing arithmetic on signed word inte-
gers, positive overflow can occur when the true signed result is larger than 16 bits.
The MMX technology provides three ways of handling out-of-range conditions:

•

Wraparound arithmetic — With wraparound arithmetic, a true out-of-range result is truncated (that is, the
carry or overflow bit is ignored and only the least significant bits of the result are returned to the destination).
Wraparound arithmetic is suitable for applications that control the range of operands to prevent out-of-range
results. If the range of operands is not controlled, however, wraparound arithmetic can lead to large errors. For
example, adding two large signed numbers can cause positive overflow and produce a negative result.

•

Signed saturation arithmetic — With signed saturation arithmetic, out-of-range results are limited to the
representable range of signed integers for the integer size being operated on (see Table 9-1). For example, if
positive overflow occurs when operating on signed word integers, the result is “saturated” to 7FFFH, which is
the largest positive integer that can be represented in 16 bits; if negative overflow occurs, the result is
saturated to 8000H.

•

Unsigned saturation arithmetic — With unsigned saturation arithmetic, out-of-range results are limited to
the representable range of unsigned integers for the integer size. So, positive overflow when operating on
unsigned byte integers results in FFH being returned and negative overflow results in 00H being returned.

Figure 9-4. SIMD Execution Model

X3 OP Y3

X2 OP Y2

X1 OP Y1

X0 OP Y0

Source 1

Source 2

Destination