14-24 Vol. 1

PROGRAMMING WITH AVX, FMA AND AVX2

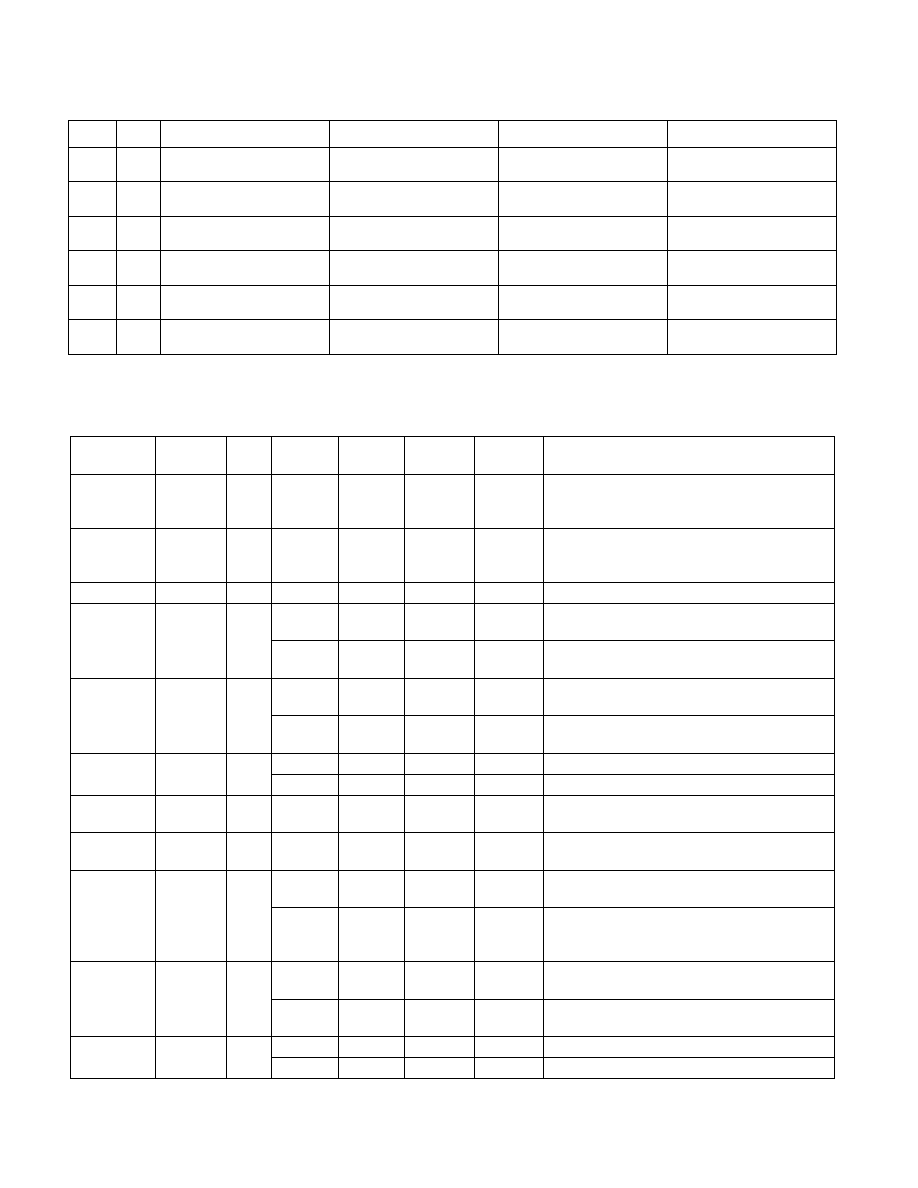
Table 14-16.  Rounding Behavior of Zero Result in FMA Operation

Table 14-17.  FMA Numeric Behavior 

x*y

z

(x*y) + z

(x*y) - z

- (x*y) + z

- (x*y) - z

(+0)

(+0)

+0 in all rounding modes

- 0 when rounding down, 

and +0 otherwise

- 0 when rounding down, 

and +0 otherwise

- 0 in all rounding modes

(+0)

(-0)

- 0 when rounding down, 

and +0 otherwise

+0 in all rounding modes

- 0 in all rounding modes

- 0 when rounding down, 

and +0 otherwise

(-0)

(+0)

- 0 when rounding down, 

and +0 otherwise

- 0 in all rounding modes

+ 0 in all rounding modes

- 0 when rounding down, 

and +0 otherwise

(-0)

(-0)

- 0 in all rounding modes

- 0 when rounding down, 

and +0 otherwise

- 0 when rounding down, 

and +0 otherwise

+ 0 in all rounding modes

F

-F

- 0 when rounding down, 

and +0 otherwise

2*F

-2*F

- 0 when rounding down, 

and +0 otherwise

F

F

2*F

- 0 when rounding down, 

and +0 otherwise

- 0 when rounding down, 

and +0 otherwise

-2*F

x 

(multiplicand)

y 

(multiplier)

z

r=(x*y)

+z

r=(x*y) 

-z

r = 

-(x*y)+z

r=

-(x*y)-z

Comment

NaN

0, F, INF, 

NaN

0, F, 

INF, 

NaN

Q(x)

Q(x)

Q(x)

Q(x)

Signal invalid exception if x or y or z is SNaN

0, F, INF

NaN

0, F, 

INF, 

NaN

Q(y)

Q(y)

Q(y)

Q(y)

Signal invalid exception if y or z is SNaN

0, F, INF

0, F, INF

NaN

Q(z)

Q(z)

Q(z)

Q(z)

Signal invalid exception if z is SNaN

INF

F, INF

+IN

F

+INF

QNaNIn

definite

QNaNInd

efinite

-INF

if x*y and z have the same sign

QNaNIn

definite

 -INF

+INF

QNaNInd

efinite

if x*y and z have opposite signs

INF

F, INF

-INF

-INF

QNaNIn

definite

QNaNInd

efinite

+INF

if x*y and z have the same sign

QNaNIn

definite

 +INF

-INF

QNaNInd

efinite

if x*y and z have opposite signs

INF

F, INF

0, F

+INF

+INF

-INF

-INF

if x and y have the same sign

-INF

-INF

+INF

+INF

if x and y have opposite signs

INF

0

0, F, 

INF

QNaNIn

definite

QNaNIn

definite

QNaNInd

efinite

QNaNInd

efinite

Signal invalid exception

0

INF

0,  F, 

INF

QNaNIn

definite

QNaNIn

definite

QNaNInd

efinite

QNaNInd

efinite

Signal invalid exception

F

INF

+IN

F

+INF

QNaNIn

definite

QNaNInd

efinite

-INF

if x*y and z have the same sign

QNaNIn

definite

-INF

+INF

 

QNaNInd

efinite

if x*y and z have opposite signs

F

INF

-INF

-INF

QNaNIn

definite

QNaNInd

efinite

+INF

if x*y and z have the same sign

QNaNIn

definite

+INF

-INF

QNaNInd

efinite

if x*y and z have opposite signs

F

INF

0,F

 +INF

+INF

-INF

 -INF

if x * y > 0

-INF

-INF

+INF

+INF

if x * y < 0