JS1K 2018

February 2018



Fortunately, a new JS1K was organized this year, and a lot of great demos were made, and a lot of new tricks were discovered!

The theme was Coin Mine.


CSS3D maybe?

At first, I thought I could reinterpret the word "coin" with a CSS3D scene, because "coin" means "corner" in french.
So I explored CSS3D cube golfing. I managed to generate a CSS3D cube in less than 256b of RegPacked JS, then 1000 cubes or a staircase in less than 500b:

I wanted to make a MC Escher-esque scene based on this work but didn't find the right approach or time to do so. Maybe next year!

So let's see what my team actually released.

SN1KE

- PLAY
- GITHUB
- DETAILED SOURCE CODE

A few weeks before JS1k, I launched an idea on the JSgolf.club Slack room: let's try to demake my JS13kGames 2017 entry LOSSST: reduce it to the bare minimum and let's see how small it can get.

My golfing friends Xen, Xaotic, Corruptio, Subzey and p01 joined the byte-squashing party.

The game's principle is actually so simple that a 2D array (for the map) and a list of head positions (for the snake) is enough to represent all the data structures used by the game. We managed to implement the game engine (display, moves, collisions, puzzle solving) plus 25 puzzles in ~500b.
Then, we made a new version with wraps, featuring 25 wrap puzzles in ~800b.

p01 even made a 436b demake's demake, rendered in ASCII!

The size difference between both wrap and non-wrap versions is mostly due to the encoding of the puzzles:

  • The no-wrap puzzles could all fit in a 6x4 grid, and after ensuring their first 4 cells were blank, the remaining 20 cells could be encoded in the bits of a single Unicode character, encoded on 3 or 4 UTF-8 bytes. 
    "ٯӟ൳ͷϼ໴𦙷࿟⛿ཿ濸ｳ񵝗𷝳𮻼𷝗𿹦򌻷򏿨򿦟񯽗𷿮񿧳" // the 25 no-wrap puzzles
  • The wrapping puzzles were a bit bigger and required more bits to be encoded, so we converted the long binary string representing each puzzle from base 2 to base 36 and saved the result in ASCII.
    The wrap puzzles also needed an explicit size (4x4, 5x5, 6x6 or 7x7) to let the game handle the wrap area properly. 
    "1hrdfddq8y,g3t6b,2tc09uicht,1ibkfyb,pesw8s3,9jorj,j7r6m,jio5o,fv5kd,jokrj,jdyrj,b2lvj,b1asx,jopxb,9luxq,d8473,jnejl,jrkbh,e03aae4,427yw3s,im7v7p,ofbd9ip,46nskug,p2yhnzn,ofaqrjz" 
// the 25 wrap puzzles

Many great byte-saving techniques were found, including:

  • Use 3ch (24px) for the squares' size, make them float to the left, and make the <body> 48ch wide, in order to wrap after each line of 16 squares. Also, use <a> elements for the squares, because <a> tags can't contain each other, so <a><a><a> produces three neighbour blocks. The "3ch" size, in particular, allows the emoji eyes to be displayed at the right size and position without any extra CSS.
  • Checking that the snake does not collide with itself, prepending a new head position (q) in the snake array (s), and saving this new position in a variable (p) is as short as: 
    s.includes(q)||s=[p=q,...s]
    . Thanks ES6!
  • Checking if a puzzle is solved is as easy as checking if every item of s is on a black square of the puzzle, basically: 
    w=s.every(p=>grid[p])}
    . Here again, thanks ES6!
  • Ensuring the snake never exceeds its max size after prepending a new head position is as easy as: 
    s.length=maxsize
    .

When JS1k started, we rewrote from scratch a game that included the 25 no-wrap and the 25 wrap puzzles, with a common game engine. We first kept the no-wrap puzzles encoded in Unicode chars and the wrap puzzles encoded in base36 ASCII chars, then realized that it took less bytes to encode all the levels in base36 and use the same decoder for both types.

Surprisingly, after a few optimizations, the whole result could fit in less than 950b! So we added 5 more wrap levels, centered the puzzles in the scene according to their size, and even made a proper game ending screen: a scrolling message saying "🎉 YOU WON! 🎉". (Thanks <marquee> tag!)

We're super happy to have been able to include so much gameplay content in 1024b.

Note: the code's entropy is so high (328b are used to encode levels data in base36, and almost no JS code is repeated in the rest of the entry) that we didn't even pack it. (Trying to pack it wouldn't have saved any bytes).


Mini Fourier

- PLAY
- GITHUB
- DETAILED SOURCE CODE

I always wanted to understand and implement 2D (image) Fourier transforms.

I studied Signal Processing at school but it has always been black magic for me, especially FFTs (Fast Fourier Transforms).
Contrary to to DFT (Discrete Fourier Transforms), FFT can compute huge amounts of Fourier transforms in just a fraction of the time.

It's pretty easy to find 1D FFT implementations in any language, some are short, some are huge, some are recursive and some are iterative.
My favourite is this one by antimatter15: it's in JS, it's iterative, and it's super tiny (about 360b minified).

A 1D Fourier Transform takes a list of numbers (generally real numbers, because they come from the real world (ex: sound samples), but it can also work on complex numbers), and it outputs a list of complex numbers representing the frequencies present in the signal.
FFTs have some little quirks: they only work on signals that have a size equal to a power of two (4, 8, 16, 32, 64, 128, 256, 512, ...), and their output is always symmetric (first == last, second == second-to-last, etc).

And that's pretty much all you can learn about it online.

But how do 2D FFT work? I found some big Github projects that perform 2D FFTs with all the options you can imagine, but I couldn't find any clear explanation on which basic operations are actually required to make them work.

Then it hit me: there's no such thing as a "2D FFT". 2D FFTs algorithms use 1D FFTs for each line and each column of an image and assemble them. How exactly? Well, here again, the Web wasn't very specific, and the people who "know" keep talking about stuff like "radix 2" and other cryptic keywords... but I finally found this very concise SO answer and went with it.

  • Take a greyscale image (each pixel has a greyscale value between 0 and 255). For example, a 256x256px image.
  • Compute the 1D FFT of each line of the image. You get 256 FFTs containing 256 complex numbers.
  • Assemble these 256 1D FFTs on a 2D grid, line by line. The grid is made of 256x256 complex numbers.
  • Take every column of this grid and compute their 1D FFT. You get 256 new FFT containing 256 complex numbers.
  • Assemble these new FFTs on a 2D grid (again), column by column.
  • Compute the magnitude of each complex number in the grid, and plot it on a canvas using a logarithmic scale (because all the values in the FFT are either super tiny or super huge, so if we didn't use this scale, the 2D FFT would be almost entirely black).

By chance, when I tried to code it, it worked on the first try!

It was fast, but it wasn't REAL TIME fast (around 80ms for a 256x256px image).

So I remembered that FFTs are symmetric, and managed to compute only half of them on the first pass and on the second pass, and completed the holes by copying all the values, mirrored, in JS, in the other half of the grid. The final plotting was also optimized by drawing only one quarter of the image, and mirroring it in the three other quarters. In the end, the computation time fell down to 25-40ms depending on the computer used. That's fast enough for a 30fps demo!

So I proceeded to make the base image drawable with the mouse, and added some options to change the thickness of the drawing (1 to 100px), its shape (round or square) and its color (black or white). The FFT was instantly computed and drawn on the side.

After forcing for a while, and with the great help of BalintCsala and Subzey, I managed to fit it in 1024b. Corruptio attempted a demake to see how small a basic, non-interactive 2D FFT could be, and reached 409b! (check out the demo HERE).

Some Math / golfing tricks to take away:

  • In the JS1K shim, you can use 
    d.write`...`
    to add HTML after a canvas without breaking its 2D context (as opposed to 
    b.innerHTML+="..."
    ).
  • If you want a reset button with free i18n, use 
    <input type=reset onclick="...">

    (it doesn't even need a value or a parent <form> to be valid).
  • Computing the magnitude of a complex number in the form ai+b can be done with 
    Math.hypot(a,b)
    . (Thanks ES6!)
  • About the logarithmic scale: the highest magnitude of the 2D FFT is saved in a variable "max",
    then we take its logarithm (
    logmax = Math.log(max)
    ).
    Finally, every complex number is drawn on a pixel with a greyscale value equal to its own magnitude divided by logmax.
    It's not necessary to ensure that the values are well between 0 and 255, it just works out of the box. 🤷‍♂️

PS: I recently discovered that JS had a native FFT method - p01 and I even used it in our 274b miniAudioviz app - though it only works with an Audio element, and I didn't find any way to feed it with arbitrary data. too bad, it would have been pretty handy to use native FFT instead of reimplementing it!


Shaderandom

- PLAY
- GITHUB
- DETAILED SOURCE CODE

I decided to rework Shaderandom (DEMO), the WebGL shader procedual generator I wrote two years ago during our WebGL quest.
I especially wanted to make this work in 1kb because it's the only project that I didn't manage to golf properly during #Golfctober 2017 (everything I tried broke the app entirely!).

So I reopened the project, annotated all the code, golfed the WebGL setup and the shader grammar as far as I could, minified it manually to avoid any Closure Compiler error, adjusted some params to have as many visual (and animated) outputs as possible, made the generated code compatible with shadertoy.com and placed it in a textarea under the canvas, so it can be read and copied easily.

No new golf tricks to share here, but a little warning about the JS1K shim's header: this header pushes down your demo's content, so be careful if you stack elements with a total height of "100vh", because if you do so, the page will overflow and scroll. (it happened to me in this demo, but I didn't have the room to fix it).


Epic cycles

- PLAY
- GITHUB
- DETAILED SOURCE CODE

During this month, a big trend appeared on Twitter (even if the concept was pretty old): drawing stuff with epicycloids.

A lot of people asked how it worked, and a lot of other people were like:
"it's super simple, just fjzfoijef a Fourier $!#@*% then xyxyyzzyxy the phase and magnitude of the complex numbers in the (){[}>)]]} and it's done!". (at least, that's the only words I understood, despite the fact that I had just made a 2D FFT demo).

Thumbs up for this blog post (in french) by ElJj explaining in detail how to draw a shape using 2 epicycloids (one for X coordinates and one for Y).

Fortunately, I found two allies in this mission, Román Cortés who gave me a clearer interpretation of the technical mumble up there, and Bálint Csala, who already helped me on MiniFourier and was also about to try and implement epicycloids on his side. So we teamed up to make this entry!

It took us a lot of different attempts, and the discovery of this github project by brettcvz to finally have a prototype running: I've put all the HTML and JS code of brettcvz in a single, 1500-line HTML page, then removed all the not mandatory parts to end up with a page structured more or less like this: 

<canvas id=a>

<script>
var points = [ /* hardcoded points of a sample "B" shape */ ];
var complex = [ ];
var gears = [ ];

// FFT.js (289 lines)
fft = (output, input) => { ... }

// epicycles.js (89 lines)
calculateGears = (complex, number) => { ... }

// simulator.js (107 lines)
render = () => { ... }

complex = fft(points);
gears = calculateGears(complex, complex.length);
render();

</script>

This worked fine! So on a separate file, we started from the end, by writing our own, simplified render loop: 

gears = [ /* hardcoded gears radii and angles used by the render loop */ ];

setInterval(
  () => {

    /* Render gears */
    
    t += 1/100;
    a.width ^= 0;
    x = centers[0][0];
    y = centers[0][1];
    for(i in complex){
      c.beginPath();
      c.arc(x, y, radii[i], 0, 7)
      c.stroke();
      c.beginPath();
      c.moveTo(x, y);
      x = centers[0][0];
      y = centers[0][1];
      for(j = 0; j <= i; j++){
        x += radii[j] * Math.cos(angles[j] + t * speeds[j]);
        y += radii[j] * Math.sin(angles[j] + t * speeds[j]);
        c.lineTo(x, y);
      }
      c.stroke();
    }
    C.lineTo(x, y);
    C.stroke();
  }, 16
)

When this worked, we started golfing calculateGears:

The secret here is that each gear corresponds to a complex number (x): the radius of the gear is equal to the magnitude of x, its initial angle is equal to the phase of x (the angle between x and the horizontal line on a 2D plane - this is computed with Math.atan2), and its speed (frequency) corrsponds to the index of x: when the first gear makes one complete cycle, the second makes two, the third three, etc. 

complex = [ /* hardcoded FFT used to compute gears */ ];
gears = [];

/* Compute gears */
centers = [[300,300]];
angles = [];
radii = [];
speeds = [1,2,3,4,5,6,7];
for(i in complex){
  radii[i] = Math.hypot(complex[i][0], complex[i][1]);
  angles[i] = Math.atan2(complex[i][0], complex[i][1]);
  if(i > 0){
    centers[i] = [centers[i-1][0] + radii[i-1], 300]; 
  }
  C.beginPath();
  C.strokeStyle = "red";
  C.lineWidth = 3;
  C.moveTo(centers[i] + radii[i], 300);
}

setInterval(
  () => {
    /* Render gears */
  }, 16
)

When this worked too, we finally attempted the most difficult part: computing the FFT of a list of hardcoded points. by chance, we could reuse the tiny implementation written by antimatter15: 

points = [ /* hardcoded points */ ]
complex = [];
gears = [];

/* Compute points FFT */
for (i = 0; Math.log2(P.length) != (Math.log2(P.length) | 0); i = (i + 2) % P.length)
  P.splice(i + 1, 0, [(P[i][0] + P[i + 1][0]) / 2, (P[i][1] + P[i + 1][1]) / 2]);
for (I = 0; I < P.length; I++) {
  for (A = J = 0, K = P.length; K >>= 1; A++)
    J = J << 1 | (I >> A & 1);
  J > I && ([P[I][0], P[J][0], P[I][1], P[J][1]] = [P[J][0], P[I][0], P[J][1], P[I][1]])
}
for (H = 1; H * 2 <= P.length; H *= 2)
  for (I = 0; I < P.length; I += H * 2)
    for (J = I; J < I + H; J++)
      E = P[J + H][0] * Math.cos(Math.PI * (J - I) / H) + P[J + H][1] * Math.sin(Math.PI * (J - I) / H),
      M = -P[J + H][0] * Math.sin(Math.PI * (J - I) / H) + P[J + H][1] * Math.cos(Math.PI * (J - I) / H),
      P[J + H][0] = P[J][0] - E,
      P[J + H][1] = P[J][1] - M,
      P[J][0] += E,
      P[J][1] += M;

for (G = [[0, Math.hypot(P[0][0], P[0][1]) / P.length, Math.atan2(P[0][1], P[0][0])]], I = 1; I <= P.length / 2; I++)
G.push(
  [I, Math.hypot(P[I][0], P[I][1]) / P.length, Math.atan2(P[I][1], P[I][0])],
  [-I, Math.hypot(P[P.length - I][0], P[P.length - I][1]) / P.length, Math.atan2(P[P.length - I][1], P[P.length - I][0])]
);
G.pop();
G.sort((A, B) => B[1] - A[1]);


/* Compute gears */

setInterval(
  () => {
    /* Render gears */
  }, 16
)

The annoying part was to ensure that there are always a number of points equal to a power of two, but Bálint had the nice idea to insert intermediate points between each successive pair of points to fill the array without changing the shape: 

for (i = 0; Math.log2(points.length) != (Math.log2(points.length) | 0); i = (i + 2) % points.length)
  points.splice(i + 1, 0, [(points[i][0] + points[i + 1][0]) / 2, (points[i][1] + points[i + 1][1]) / 2]);

Fun fact from romancortes: the gears can be chained in any order, they will always trace the same pattern. We decided to sort them from the biggest to the smallest for for more interesting visuals. (This explains why the gears speeds often appear in random order)

This entire demo (with hardcoded points) took 862b minified and packed.

After adding a rudimentary drawing feature (just click on the canvas to add points), it was up to 989b. But most importantly, we could finally generate our very own epicycloids!

So we started adding cool stuff in the demo... and golfing it at the same time: 1037b after including a build-in JS1K logo, 1023b after making the canvas fullscreen and compressing all the points into ASCII chars (first, one char per coordinate, then one char for both X and Y), 1042b after adding keyboard controls, 1010b after optimizing the gears generation with a pen and a piece of paper, 1051b after implementing a nicer drawing UI (click - move - release), etc...

Then we hit a barrier: we wanted to implement some cool features (like avoiding to draw dozens of points too close to each other by moving the mouse slowly for example), but we couldn't free enough bytes to add them.

Fortunately, Bálint found a way to implement DCT instead of FFT, which suddenly made our demo fall to 930b! (DCT is longer, but it actually requires much less code than FFT). 

// Compute the DFT of P.
// This is black magic inspired by Paul Bourke's C++ code.
_ = [];
for (i in P) {
  _[i] = [0, 0];
  for (k in P)
    // Perform complex rotations or something like that?
    _[i][0] += (P[k][0] * Math.cos(k * -2 * Math.PI * i / P.length) - P[k][1] * Math.sin(k * -2 * Math.PI * i / P.length)),
    _[i][1] += (P[k][0] * Math.sin(k * -2 * Math.PI * i / P.length) + P[k][1] * Math.cos(k * -2 * Math.PI * i / P.length));
}

This allowed us to do all the little enhancements we wanted to do, and even put a black background to the page, while the lines were being traced in white.

We're very happy with the result!

In the meantime, 3blue1brown published a great video showing why FFTs are so associated with rotations. Watching this video suddenly made epicycloids make a lot of sense: the Fourier transform "rolls" the points on a circle, and the epicycloids just do the opposite operation.

After JS1K, Bálint published a similar tool with a much nicer UI (and many extra kilobytes): CircleMachine.

To finish, here are some of our creations:




MUS1K

- PLAY
- GITHUB
- DETAILED SOURCE CODE

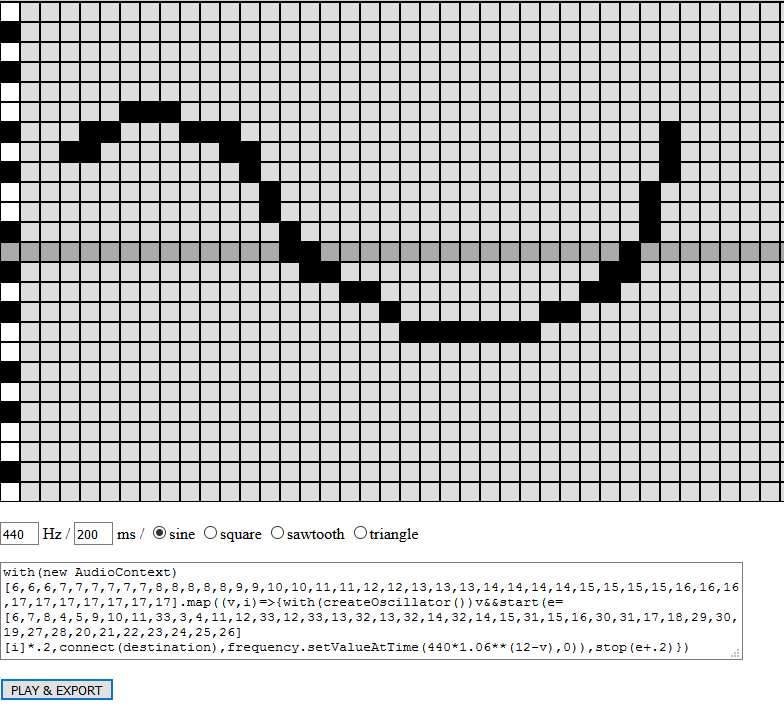
During the last week of the contest, I saw this entry, aiming to create a melody with the mouse and play it.

It reminded me MiniMusic, a tool I hacked in a couple hours before the beginning of JS13kGames 2017.

So I tried to fit that tool in 1kb, without removing any feature, and it worked!

I even added one important change in the generated code snippet: replacing 

frequency.value = f
(which is now deprecated) with 
frequency.setValueAtTime(f, 0)
.

One little quirk though, about the JS1K shim: the <body>'s margin are forced to 0px, and my attempts to give the page a little margin (with 

#b{margin:1em}
or 
body{margin:1em}
) failed. The first one failed because the body element doesn't have an id equal to "b", it's just a reference of the body that is stored in b. The second one failed because the body had an inline CSS rule forcing its margin to 0px, and inline CSS is stronger than CSS placed in <style> elements.

I should have used padding, but didn't have the idea before submitting the entry. 🤷‍♂️


BONUS (not submitted): 1KB NES ROM DISASSEMBLER

- DEMO
- GITHUB
- DETAILED SOURCE CODE

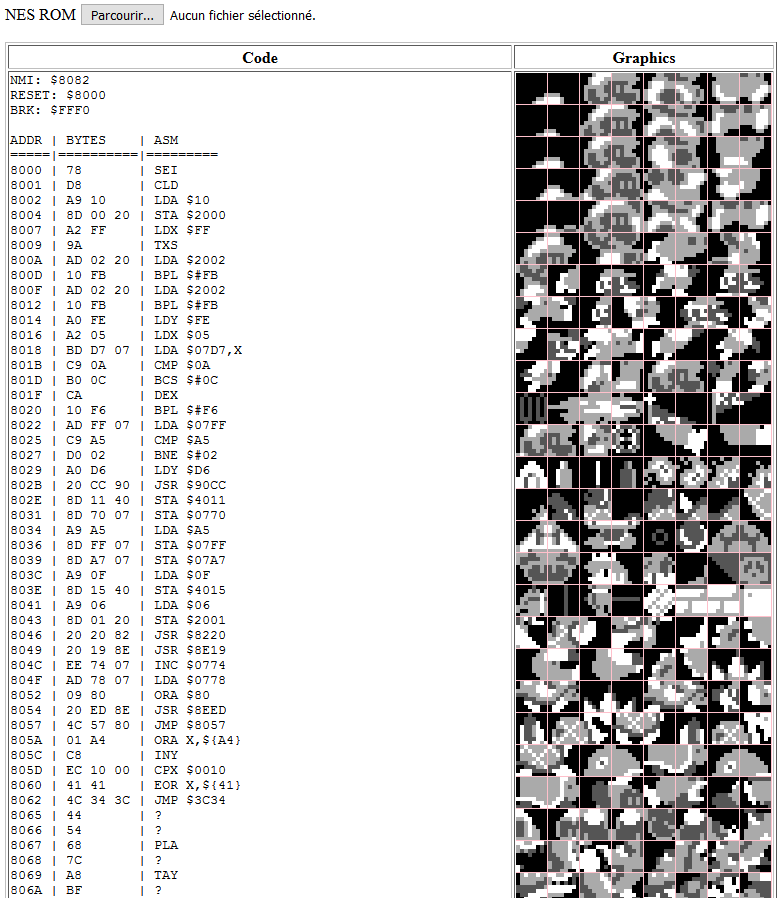
At the beginning of the month, I went a little crazy, imagining that I could make the level 1-1 of Super Mario Bros in 1kb, or maybe a mini NES emulator in 1kb (I guess I was inspired by this epic NES emulator coded in 15 minutes).

It would have been in the theme because, you know, Mario collects coins and stuff, but of course, it was not possible.

Though I read a lot of documentation on NES emulation and realized that I could at least do one fun thing: a 1KB NES ROM disassembler, displaying all the program memory in the form of assembler code, and all the graphic memory in the form of consecutive 8x8px sprites, drawn on a canvas.

It was a bit ambitious, but it worked!
...I mean, I could make this disassembler fit in a 1Kb zip file.

Sadly, it was too big to fit unzipped (or regpacked) in a JS1K shim, so I didn't submit it.


(Awesome) results!

see you next year!