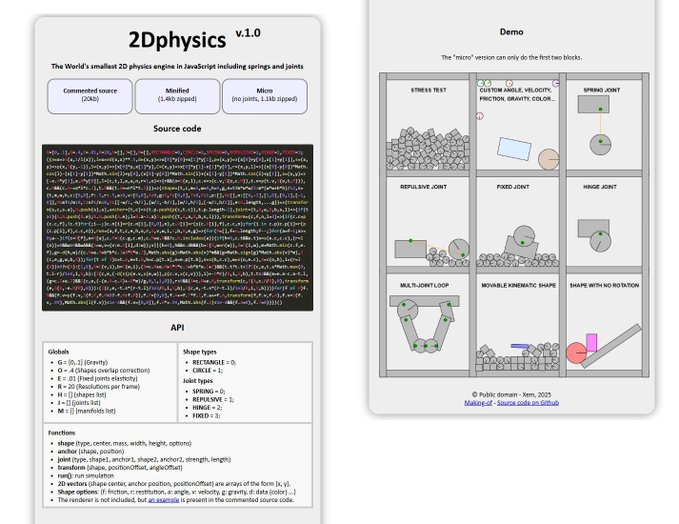
Golfing a 2D physics engine in JS
November-December 2025
Introduction
I have a long love-hate story with physics in JS.
It all started in 2019, when I read this 134 pages book about 2D physics, and summarized its contents in just 9 pages on my little notepad.
I used that to create a 1.57kb lib called Mini2DPhysics, the JS1K entry Emojysics in 2019 and the JS13kGames entry O HIII BAD SKATEPARK in 2024.
The problem was that this book, as every book I could find at the time, didn't go beyond basic interactions between discs and rectangles (and it definitely didn't need so many pages to do that).
Then this 599 pages book released in 2022 by the same editor and some of the original authors, managed to be even more verbose in almost every aspect of 2D game mechanics, except one: advanced physics. And when I say "advanced physics", I'm not asking for really complex stuff, I just want to learn springs, fixed joints, hinge joints, and how to optimize for speed and stability.
In 2021, 2022, 2023, 2024 and 2025 I tried many times to learn 3D physics because a lot of good books actually cover this topic, but I haven't managed to completely implement any of them in JS (so far)... which was quite frustrating. (but stay tuned... I will be back!)
Finally, in October 2025, after completing a new edition of JS13KGames, I randomly typed "2D physics JS" on Google and stumbled upon this 2024 Reddit post announcing a complete Youtube playlist dedicated to learning 2D physics in JS, with complete source code on Gitlab... I may have found the holy grail!
In this page, I will follow each chapter of the playlist, show how I implemented my own mini 2D engine based on its source code, and how I enhanced a few things. My code will be published in public domain on the 2DPhysics Github repo, and a copy of the original Gitlab repo is also present there for reference..
I also ended up buying a copy of the physical book released in August 2025, which is (sadly) just a line-by-line code explanation written by an AI, with a lot of mistakes. I won't mention it here, but I still really encourage the author to pursue his work (and teach us how to do 3D physics in JS next!), because my 2Dphysics engine mostly exists thanks to him! And if he makes a new edition of his book with better page layout, more legible text and some illustrations, I will gladly buy it too! <3
CODING MY OWN ENGINE
Chapter 1: Setting up a Canvas
Here we'll keep the HTML code to the absolute minimum: doctype, canvas and script tags.
The canvas is called a and its 2D context c.
<!doctype html>
<canvas id=a width=800 height=600 style="background:#eee"></canvas>
<script>
// Canvas setup
c = a.getContext("2d");
</script>Links:
- Original:
video,
demo,
source code (0.4kb)
- Mine:
demo (nothing to see yet),
source code (0.1kb)
From now on, the code snippets in each chapter will only show what was added or modified in my Javascript code.
Chapter 2: Main loop
Let's create a fixed 60fps loop with setInterval, for simplicity.
Indeed, many 2D game engines use requestAnimationFrame and deltaTime, but it's more verbose, non-deterministic, and tends to be unpredictable on screens with high refresh rates.
A fixed loop will allow a consistent and reproductible behavior on all kinds of screens, with just a little lisk of lag on low-end devices if the game is not optimized enough.
// Main loop
setInterval(() => {
// TODO
}, 16);Links:
- Original:
video,
demo,
source code (1.3kb)
- Mine:
demo (nothing to see yet),
source code (0.2kb)
Chapter 3: Mouse and keyboard events
User inputs and states are reduced to the bare minimum: left and right mouse buttons and mouse position. Two functions are added in the loop: update and draw.
// Globals
m = null, mp = 0; // mouse position, pressed
// Event listeners
onmousemove = e => {
m = {x: e.pageX - a.offsetLeft, y: e.pageY - a.offsetTop};
}
onmousedown = e => {
mp = 1;
}
onmouseup = e => {
mp = 0;
}
// Update the physics engine
update = () => {
console.log(m); // Test logs
}
// Render the scene
draw = () => {
// Reset canvas
a.width = a.width;
// Test: draw a black square
c.fillRect(100, 100, 20, 20);
}
// Main loop
setInterval(() => {
update();
draw();
}, 16);Links:
- Original:
video 1,
2,
demo,
source code (2.8kb)
- Mine:
demo (only shows a rectangle),
source code (0.7kb)
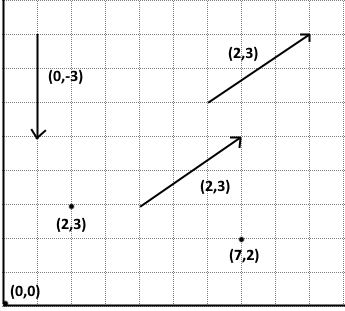Chapter 4: 2D vectors
2D vectors are objects containing two values (x and y).
They can represent a point (with x and y coordinates) or a movement (with x and y offsets).
I will reuse the mini vector lib I created for Mini2DPhysics, adapted to this new tutorial.
The mouse position can now be stored as a Vec2.
// 2D vectors
Vec2 = (x, y) => ({x, y});
normalize = v => scale(v, 1 / len(v));
len = v => dot(v, v) ** .5;
len2 = v => dot(v, v);
normal = v => Vec2(v.y, -v.x);
dot = (v, w) => v.x * w.x + v.y * w.y;
copy = v => Vec2(v.x, v.y);
add = (v, w) => Vec2(v.x + w.x, v.y + w.y);
sub = (v, w) => add(v, scale(w, -1));
scale = (v, n) => Vec2(v.x * n, v.y * n);
// Event listeners
onmousemove = e => {
m = Vec2(e.pageX - a.offsetLeft, e.pageY - a.offsetTop);
}Links:
- Original: video
demo,
source code (3.8kb)
- Mine:
demo (nothing more to see),
source code (1.0kb)
Chapter 5: Drawing points and arrows
Thie tuto explains how do draw bullets (filled arcs), discs (stroked arcs), lines and arrows, for debug purposes.
We'll settle with just two methods: drawPoint and drawLine.
// Debug
drawPoint = (center, radius = 5, color = "#888") => {
c.beginPath();
c.fillStyle = color;
c.arc(center.x, center.y, radius, 0, 7);
c.fill();
c.closePath();
}
drawLine = (start, end, color = "#888") => {
c.beginPath();
c.lineWidth = 3;
c.strokeStyle = color;
c.moveTo(start.x, start.y);
c.lineTo(end.x, end.y);
c.stroke();
c.closePath();
}
// Render the scene
draw = () => {
// Reset canvas
a.width = a.width;
// Test: draw some shapes
c.fillRect(100, 100, 20, 20);
drawPoint(Vec2(200,200));
drawLine(Vec2(300, 50), Vec2(400, 150));
}Links:
- Original:
video 1,
2,
3,
demo,
source code (5.6kb)
- Mine:
demo,
source code (1.4kb)
Chapter 6: Shapes
This chapter introduces a generic Shape class for circles and polygons.
We'll make our own version in Chapter 8.
Links:
Original:
video
demo,
source code (7.2 kb)
Chapter 7: Compute the centroid of a polygon
We don't need this here: as all our shapes will be based on circles and rectangles, which already have a defined center point.
Links:
Original:
video 1,
2,
demo,
source code (7.2 kb)
Chapter 8: Rotating and moving shapes
Here, we start implementing our shape objects (circles and rectangles) and the methods that allow them to translate (move) and rotate.
Rectangles have 4 vertices (points) and 4 edges (sides).
- Translations are performed by adding an offset vector to the shape's center (and to all its vertices, if it's a rectangle).
- 2D rotations (around the origin [0,0]) are performed by applying a 2D rotation matrix on 2D vectors.
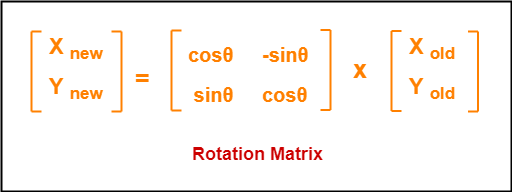
- 2D rotations around a pivot point are done by subtracting the pivot point's coordinates from the point, rotating the point around the origin, and adding the pivot point back. A rotate function is added to perform these kinds of rotations.
A horizontal radius is drawn on the discs to make their rotations visible.
Realistic rotations based on gravity, friction and inertia will be introduced in chapter 24.
// Globals
shapes = [];
// 2D vectors
rotate = (v, center, angle) => {
var x = v.x - center.x;
var y = v.y - center.y;
return Vec2(
x * Math.cos(angle) - y * Math.sin(angle) + center.x,
x * Math.sin(angle) + y * Math.cos(angle) + center.y
);
}
// Shapes
circle = (center, radius, angle = 0, color = "#888") => {
shape = {
type: "circle",
center: center,
radius: radius,
angle: angle,
color: color
};
shapes.push(shape);
return shape;
}
rectangle = (center, width, height, angle = 0, color = "#888") => {
shape = {
type: "rectangle",
center: center,
width: width,
height: height,
angle: angle,
color: color,
// Rectangle vertices
vertices: [
Vec2(center.x - width / 2, center.y - height / 2), // top left
Vec2(center.x + width / 2, center.y - height / 2), // top right
Vec2(center.x + width / 2, center.y + height / 2), // bottom left
Vec2(center.x - width / 2, center.y + height / 2) // bottom right
]
};
if(angle) {
rotateShape(shape, angle);
}
shapes.push(shape);
return shape;
};
// Translate a shape
translateShape = (shape, offset) => {
// Move center
shape.center = add(shape.center, offset);
// Rectangle (move vertices)
if(shape.type == "rectangle"){
for(var i in shape.vertices){
shape.vertices[i] = add(shape.vertices[i], offset);
}
}
}
// Rotate a shape around its center
rotateShape = (shape, angle) => {
// Update angle
shape.angle += angle;
// Rectangle (rotate vertices)
if(shape.type == "rectangle"){
for(var i in shape.vertices){
shape.vertices[i] = rotate(shape.vertices[i], shape.center, angle);
}
}
}
// Update the physics engine
update = () => {
// Test: translate and rotate the shapes
for(var i of shapes){
rotateShape(i, .01);
translateShape(i, Vec2(.2, .2));
}
}
// Render the scene
draw = () => {
// Reset canvas
a.width = a.width;
// Draw shapes
for(var i of shapes){
c.save();
c.beginPath();
if(i.type == "circle"){
c.fillStyle = i.color;
c.translate(i.center.x, i.center.y);
c.rotate(i.angle);
c.arc(0, 0, i.radius, 0, 7);
c.lineTo(0,0);
c.closePath();
c.fill();
c.stroke();
}
else if(i.type == "rectangle"){
c.fillStyle = i.color;
c.moveTo(i.vertices[0].x, i.vertices[0].y);
c.lineTo(i.vertices[1].x, i.vertices[1].y);
c.lineTo(i.vertices[2].x, i.vertices[2].y);
c.lineTo(i.vertices[3].x, i.vertices[3].y);
c.closePath();
c.fill();
c.stroke();
}
c.restore();
}
}
// Demo
circle(Vec2(100, 100), 60);
rectangle(Vec2(250, 100), 60, 100);Links:
- Original:
video 1,
2,
demo,
source code (10.8 kb)
- Mine:
demo,
source code (3.9 kb)
Chapter 9: Circle-circle collision detection
The real work starts here!
A physics engine has two main tasks: collision detection and collision response. Let's start with detection.
All our shapes will be either circles or rectangles, so we need to detect three kinds of collisions: circle-circle, circle-rectangle and rectangle-rectangle.
We'll start by the easiest collision detection, between two circles: if the distance between their centers is smaller than the sum of their radii, they are colliding.
In the code below, two circles are created (c1 and c2), a distance function dist is added and when the circles collide, they get colored in red. The collision detection is just one line in the update method, but it will be more complete in the next chapters.
// 2D vectors
dist = (v, w) => len(sub(v, w));
// Update the physics engine
update = () => {
// Test: rotate all shapes
for(var i of shapes){
rotateShape(i, .01);
}
// Test: translate each shape
translateShape(c1, Vec2(-.2, .2));
translateShape(c2, Vec2(.2, .2));
// Test: detect circle-circle collisions
if(c1.type == "circle" && c2.type == "circle"){
if(dist(c1.center, c2.center) < (c1.radius + c2.radius)){
c1.color = "red";
c2.color = "red";
}
else {
c1.color = "#888";
c2.color = "#888";
}
}
}
// Demo
c1 = circle(Vec2(220, 140), 60);
c2 = circle(Vec2(80, 100), 60);Links:
- Original:
video,
demo,
source code (11.8 kb)
- Mine:
demo,
source code (4.3 kb)
Chapter 10: Collision manifolds
Physics engines use temporary objects called manifolds to store information about a collision between two shapes. They include:
- a penetration depth (overlap distance)
- a collision normal (the force's direction, from one shape's contact point to the other shape's center)
- and a contact point (where the collision takes place on the surface of the first shape)
For each pair of shapes that collide, a single manifold object is created. Both shapes will respond to the same manifold: shape A will use the collision normal to move away from shape B, and B will use the inverse of the collision normal to move away from A.
Here, our debug methods drawPoint and drawLine are used to show the manifold information, in blue.
// Globals
manifold = null;
// Update the physics engine
update = () => {
// (...)
// Test: detect circle-circle collisions
if(c1.type == "circle" && c2.type == "circle"){
direction = sub(c2.center, c1.center);
distance = dist(c1.center, c2.center);
if(distance < (c1.radius + c2.radius)){
manifold = {
depth: (c1.radius + c2.radius) - distance,
normal: normalize(direction),
contactPoint: add(c1.center, scale(normalize(direction), c1.radius))
};
c1.color = "red";
c2.color = "red";
}
else {
c1.color = "#888";
c2.color = "#888";
manifold = null;
}
}
}
// Render the scene
draw = () => {
// (...)
// Debug: draw manifold
if(manifold){
drawPoint(manifold.contactPoint, 5, "#04F");
drawLine(manifold.contactPoint, add(manifold.contactPoint, scale(manifold.normal, 50)), "#04F");
}
}
// Demo (inversed the circles temporarily to display c1 on top of c2)
c2 = circle(Vec2(80, 100), 60);
c1 = circle(Vec2(220, 140), 60);Links:
- Original:
video,
demo,
source code (12.2 kb)
- Mine:
demo,
source code (4.9 kb)
Chapter 11: Pushing circles apart
Pushing overlapping shapes apart is the first mechanism that takes action in a collision response.
It's possible to have just one shape being pushed, or both, depending on their mass or mobility.
For example here, only one shape (c2) is pushed, while the other (c1) keeps moving diagonally.
The pushing mechanism will be implemented more rigorously in chapter 23.
// Update the physics engine
update = () => {
// (...)
// Test: translate one shape
translateShape(c1, Vec2(.2, .2));
// Test: detect circle-circle collisions
if(c1.type == "circle" && c2.type == "circle"){
direction = sub(c2.center, c1.center);
distance = dist(c1.center, c2.center);
if(distance < (c1.radius + c2.radius)){
manifold = {
depth: (c1.radius + c2.radius) - distance,
normal: normalize(direction),
contactPoint: add(c1.center, scale(normalize(direction), c1.radius))
};
// Push c2
c2.center = add(c2.center, scale(manifold.normal, manifold.depth));
c1.color = "red";
c2.color = "red";
}
else {
c1.color = "#888";
c2.color = "#888";
manifold = null;
}
}
}Links:
- Original:
video 1,
2
demo,
source code (13 kb)
- Mine:
demo,
source code (4.9 kb)
Chapter 12: Compute polygons normals
For rectangles (and other polygons), each edge (side) needs a normal vector, perpendicular to it and facing outwards, to compute collisions.
The normals stay the same when the rectangle is translated, but they must be recomputed when it's rotated.
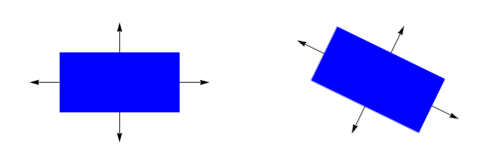
In the code below, a rectangle r1 is introduced. Its normals are represented in green.
// shapes
rectangle = (center, width, height, angle = 0, color = "#888") => {
// (...)
// Normals
calcNormals(shape);
shapes.push(shape);
return shape;
};
// Rotate a shape around its center (angle in radians)
rotateShape = (shape, angle) => {
// Update angle
shape.angle += angle;
// Rectangle (rotate vertices and recompute normals)
if(shape.type == "rectangle"){
for(var i in shape.vertices){
shape.vertices[i] = rotate(shape.vertices[i], shape.center, angle);
}
calcNormals(shape);
}
}
// Compute the normals of a polygon
calcNormals = shape => {
shape.normals = [];
for(var i = 0; i < shape.vertices.length; i++){
shape.normals.push(normal(normalize(sub(shape.vertices[(i + 1) % shape.vertices.length], shape.vertices[i]))));
}
}
// Render the scene
draw = () => {
// Reset canvas
a.width = a.width;
// Draw shapes
for(var i of shapes){
c.save();
c.beginPath();
if(i.type == "circle"){
// (...)
}
else if(i.type == "rectangle"){
// (...)
// Test: draw normals
for(j = 0; j < 4; j++){
middle = scale(sub(i.vertices[(j + 1) % i.vertices.length], i.vertices[j]), .5);
drawLine(add(i.vertices[j], middle), add(add(i.vertices[j], middle), scale(i.normals[j], 30)), "green");
}
}
c.restore();
}
// (...)
}Links:
- Original:
video 1,
2
demo,
source code (13.6 kb)
- Mine:
demo,
source code (4.7 kb)
Chapter 13: Rectangle-rectangle collisions
Collisions between rectangles (or any convex polygons) are detected using the Seprating-Axis Theorem (SAT):
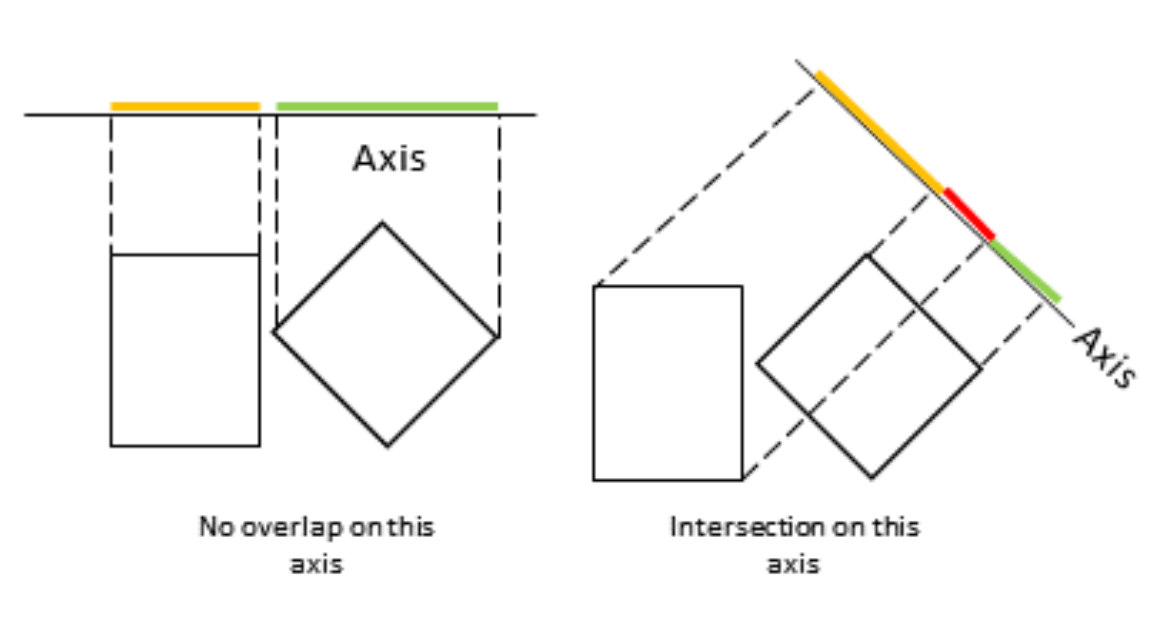
The idea is to project a pair of rectangles on different axis (one axis for each edge of each polygon to test).
- If the projections are separated on at least one axis, the shapes are definitely not colliding.
- If the projections overlap on every axis, the shapes collide. We use the axis with the smallest overlap to build the collision manifold.
Contrary to circle-circle collisions, the collision normal does not point to the center of the other shape: it is perpendicular to the rectangle edge that has the smallest penetration depth.
In this chapter, we create three rectangles, and for each pair of rectangles, if a collision is detected, both shapes get pushed away from each other with the same force.
The manifolds are drawn on the first vertex of the axis that detects the collision.
// Globals
manifolds = [];
// SAT: test two rectangles against each other's axis and choose the minimal penetration depth
rectangleRectangleCollision = (r1, r2) => {
var contact = null;
// Check all axes from rectangle A against rectangle B
var contactA = getContactPoint(r1, r2);
if(contactA == null) return null;
// Check all axes from rectangle B against rectangle A
var contactB = getContactPoint(r2, r1);
if(contactB == null) return null;
// Choose the smallest penetration depth (most restrictive axis)
if(contactA.depth < contactB.depth){
contact = contactA;
}
else {
contact = contactB;
// Reverse the normal direction to ensure it points from A to B
contact.normal = scale(contact.normal, -1);
}
// Return the final contact information (depth, normal, contact point)
return contact;
}
// SAT: Test all normals of rectangle 1 as potential separating axes
getContactPoint = (r1, r2) => {
var contact = null;
var minDepth = Number.MAX_VALUE;
var supportPoint = null;
// For each normal of rectangle 1
for(var i = 0; i < r1.normals.length; i++){
// Find which vertex of rectangle 2 penetrates deepest along this normal
supportPoint = findSupportPoint(r1.normals[i], r1.vertices[i], r2.vertices);
// If there is no overlap along this normal, there is no collision
if(supportPoint == null) return null;
// Keep the smallest penetration depth found so far
if(supportPoint.depth < minDepth){
minDepth = supportPoint.depth;
// Store the contact information for this axis
contact = {
depth: minDepth, // penetration distance
normal: r1.normals[i], // collision normal (axis of penetration)
contactPoint: supportPoint.vertex // point of contact on rectangle 2
};
}
}
// Return the axis with the minimum overlap
return contact;
}
// SAT: Find which vertex from the other rectangle penetrates the deepest along a given axis
findSupportPoint = (normalOnEdge, pointOnEdge, otherPolygonVertices) => {
var maxDepth = 0;
var supportPoint = null;
var depth = null;
// For each vertex of the other rectangle
for(var i = 0; i < otherPolygonVertices.length; i++){
// Project the vertex onto the axis defined by the current normal
// The 'depth' here represents how far the vertex is behind the edge (penetration distance)
depth = dot(sub(otherPolygonVertices[i], pointOnEdge), scale(normalOnEdge, -1));
// Keep the vertex that penetrates the most (maximum depth)
if(depth > maxDepth){
maxDepth = depth;
supportPoint = {
vertex: otherPolygonVertices[i], // the vertex with the deepest penetration
depth: depth // its penetration distance
};
}
}
// Return the vertex that is deepest along this normal
return supportPoint;
}
// Update the physics engine
update = () => {
var push, manifold;
// Reset manifolds
manifolds = [];
// Reset shapes colors
for(var i of shapes){
i.color = "#888";
}
// Test: rotate a shape
rotateShape(r1, -.01);
// Test: translate a shape
translateShape(r1, Vec2(.2, .2));
// Consider all pairs of shapes
for(var i = 0; i < shapes.length; i++){
for(var j = i; j < shapes.length; j++){
if(i != j){
// Detect rectangle-rectangle collisions
if(shapes[i].type == "rectangle" && shapes[j].type == "rectangle"){
manifold = rectangleRectangleCollision(shapes[i], shapes[j]);
if(manifold){
shapes[i].color = "red";
shapes[j].color = "red";
push = scale(manifold.normal, manifold.depth * 0.5);
translateShape(shapes[j], push);
translateShape(shapes[i], scale(push, -1));
manifolds.push(manifold);
}
}
}
}
}
}
// Render the scene
draw = () => {
// (...)
// Debug: draw manifolds
for(var i of manifolds){
drawPoint(i.contactPoint, 5, "#04F");
drawLine(i.contactPoint, add(i.contactPoint, scale(i.normal, 50)), "#04F");
}
}
// Demo
r1 = rectangle(Vec2(100, 60), 100, 50);
r2 = rectangle(Vec2(180, 170), 75, 75);
r3 = rectangle(Vec2(240, 150), 20, 50);Links:
- Original:
video 1,
2
3
demo,
source code (16.4 kb)
- Mine:
demo,
source code (8.3 kb)
Chapter 14: Circle-rectangle collisions
To detect a collision between a rectangle and a circle, we need to find which point of the rectangle is closest to the center of the circle.
This point can be a corner, or any point on one edge of the rectangle.
// Detect collision between a circle and a rectangle
circleRectangleCollision = (circle, rectangle) => {
// First, try to detect a collision between the circle and the rectangle's edges
var contact = circleVsRectangleEdges(circle, rectangle);
// If no edge collision was found, test against the rectangle's corners
if(!contact){
contact = circleVsRectangleCorners(circle, rectangle);
}
// Return the resulting contact information (if any)
return contact;
}
// Test collision between a circle and the edges of a rectangle
circleVsRectangleEdges = (circle, rectangle) => {
var nearestEdgeVertex = null;
var nearestEdgeNormal = null;
var dirToNext, circleDirToNextProjection, circleDirToNormalProjection;
// Loop over each edge of the rectangle
for(var i = 0; i < rectangle.vertices.length; i++){
// Vector from the current vertex of the rectangle to the circle center
vertToCircle = sub(circle.center, rectangle.vertices[i]);
// Direction vector along the current edge
dirToNext = sub(rectangle.vertices[(i + 1) % rectangle.vertices.length], rectangle.vertices[i]);
// Project the circle center direction onto the edge direction
circleDirToNextProjection = dot(vertToCircle, normalize(dirToNext));
// Project the circle center direction onto the edge normal
circleDirToNormalProjection = dot(vertToCircle, rectangle.normals[i]);
// Check if the circle center is within the edge segment bounds
// (projection along the edge is between 0 and edge length)
// and on the "inner" side of the edge (normal projection ≥ 0)
if(circleDirToNormalProjection >= 0 && circleDirToNextProjection > 0 && circleDirToNextProjection < len(dirToNext)){
// This edge is the nearest potential collision candidate
nearestEdgeNormal = rectangle.normals[i];
nearestEdgeVertex = rectangle.vertices[i];
}
}
// If no valid edge was found, no collision is possible along edges
if(nearestEdgeNormal == null || nearestEdgeVertex == null){
return null;
}
// Compute how far the circle center is from the edge along the normal
var projectionToEdgeNormal = dot(nearestEdgeNormal, sub(circle.center, nearestEdgeVertex));
// If the circle overlaps the edge (distance < radius), report a collision
if(projectionToEdgeNormal - circle.radius < 0){
return {
// Penetration depth (how far the circle intrudes)
depth: -(projectionToEdgeNormal - circle.radius),
// Normal points from rectangle toward the circle
normal: scale(nearestEdgeNormal, -1),
// Approximate contact point on the circle’s perimeter
contactPoint: add(circle.center, scale(nearestEdgeNormal, -circle.radius))
};
}
// No edge collision
return null;
}
// Test collision between a circle and the corners of a rectangle
circleVsRectangleCorners = (circle, rectangle) => {
var dirToCircleCenter;
// Loop over all rectangle vertices
for(var i = 0; i < rectangle.vertices.length; i++){
// Vector from the circle center to the current corner
dirToCircleCenter = sub(rectangle.vertices[i], circle.center);
// If the corner is inside the circle’s radius, a collision occurs
if(len2(dirToCircleCenter) < (circle.radius ** 2)){
return {
// Penetration depth (difference between radius and distance)
depth: circle.radius - len(dirToCircleCenter),
// Normal pointing from circle center toward the corner
normal: normalize(dirToCircleCenter),
// Contact point is the rectangle corner itself
contactPoint: rectangle.vertices[i]
};
}
}
// No corner inside the circle → no collision
return null;
}
// Update the physics engine
update = () => {
var push, manifold, circle, rectangle, shape1, shape2;
// Reset manifolds
manifolds = [];
// Reset shapes colors
for(var i of shapes){
i.color = "#888";
}
// Test: rotate a shape
rotateShape(r1, -.01);
// Test: translate a shape
translateShape(r1, Vec2(.2, .1));
// Consider all pairs of shapes
for(var i = 0; i < shapes.length; i++){
for(var j = i; j < shapes.length; j++){
if(i != j){
shape1 = shapes[i];
shape2 = shapes[j];
// Detect circle-rectangle collisions
if(shapes[i].type == "rectangle" && shapes[j].type == "circle"){
rectangle = shapes[i];
circle = shapes[j];
manifold = circleRectangleCollision(circle, rectangle);
}
else if(shapes[i].type == "circle" && shapes[j].type == "rectangle"){
circle = shapes[i];
rectangle = shapes[j];
manifold = circleRectangleCollision(circle, rectangle);
}
// Collision response
if(manifold){
shape1.color = "red";
shape2.color = "red";
push = scale(manifold.normal, manifold.depth * 0.5);
translateShape(rectangle, push);
translateShape(circle, scale(push, -1));
manifolds.push(manifold);
}
}
}
}
}
// Demo
r1 = rectangle(Vec2(80, 60), 120, 50);
c2 = circle(Vec2(180, 130), 50);Links:
- Original:
video 1,
2
3
demo,
source code (19.1 kb)
- Mine:
demo,
source code (12.2 kb)
Chapter 15: RigidBody
Rigid bodies add new peoperties to our shapes: mass, invMass, velocity and forceAccumulator.
Mass is a number representing the object's weight.
Velocity is a Vec2 representing the object's speed (evolution of position over time).
Acceleration is the evolution of velocity over time.
According to Newton's 2nd law of motion (F = ma or a = F/m), the acceleration of an object is equal to the sum of the forces applied to it (pushes, gravity, friction...), divided by its mass.
The forceAccumulator Vec2 attribute is introduced to represent this sum of forces. It will be reset after each frame.
An invMass (1/mass) attribute is introduced specifically to avoid doing the "F/m" division repeatedly.
// Shapes
circle = (center, radius, mass = 1, angle = 0, velocity = Vec2(0, 0), color = "#888") => {
shape = {
type: "circle",
center: center,
radius: radius,
mass: mass,
invMass: 1 / mass,
velocity: velocity,
angle: angle,
forceAccumulator: Vec2(0, 0),
color: color
};
shapes.push(shape);
return shape;
}
rectangle = (center, width, height, mass = 1, angle = 0, velocity = Vec2(0, 0), color = "#888") => {
shape = {
type: "rectangle",
center: center,
width: width,
height: height,
mass: mass,
invMass: 1 / mass,
velocity: velocity,
angle: angle,
forceAccumulator: Vec2(0, 0),
color: color,
// (...)
};Links:
- Original:
video,
demo,
source code (19.4 kb)
- Mine:
demo (nothing new to see yet), source code (12.6 kb),
Chapter 16: Combining RigidBody and Shapes
We've already done that in chapter 15.
Links:
Original:
video,
demo,
source code (18.9 kb)
Chapter 17: Integration
Integration consists in computing the shapes' acceleration, velocity and position at the end of a frame.
The code below uses the semi-implicit Euler method, which is a good compromise between simplicity and stability.
According to Newton's first law of motion, objects keep the same trajectory and speed as long as they don't encounter another force.
Until gravity and friction get implemented, the shapes will keep a constant speed after a collision.
In the original code, acceleration and velocity are proportional to deltaTime. Here, with setInterval, it can remain constant.
// Shape integration
integrate = (shape) => {
// compute acceleration
var acceleration = scale(shape.forceAccumulator, shape.invMass);
// apply acceleration to velocity
shape.velocity = add(shape.velocity, acceleration);
// apply velocity to position
translateShape(shape, shape.velocity);
// reset force accumulator
shape.forceAccumulator = Vec2(0, 0);
}
// Update the physics engine
update = () => {
// (...)
// Collision response
if(manifold){
shape1.color = "red";
shape2.color = "red";
push = scale(manifold.normal, manifold.depth * 0.5);
rectangle.forceAccumulator = add(rectangle.forceAccumulator, push);
circle.forceAccumulator = add(circle.forceAccumulator, scale(push, -1));
manifolds.push(manifold);
}
// (...)
// Integration
for(i of shapes){
integrate(i);
}
}Links:
- Original:
video,
demo,
source code (19.1 kb)
- Mine:
demo,
source code (13.0 kb)
Chapter 18: Other integration methods
This chapter explores other ways to integrate rigid bodies. We can ignore it.
Links:
Original:
video 1,
2
demo,
source code (21.1 kb)
Chapter 19: Bouncing balls
Let's make balls behave realistically with bouncing and damping (velocity attenuation over time)
The bouncing on the ground is currently implemented by inverting the ball's velocity when it reaches a certain height threshold.
// Shape integration
integrate = (shape) => {
// compute acceleration
var acceleration = scale(shape.forceAccumulator, shape.invMass);
// apply acceleration to velocity
shape.velocity = add(shape.velocity, acceleration);
// apply velocity to position
translateShape(shape, shape.velocity);
// reset force accumulator
shape.forceAccumulator = Vec2(0, 0);
// velocity damping
shape.velocity = scale(shape.velocity, .99);
}
// Update the physics engine
update = () => {
// (...)
// Ball update
for(i of shapes){
// Apply gravity
i.forceAccumulator = add(i.forceAccumulator, gravity);
// Integration
integrate(i);
// Bouncing (temp)
if(i.center.y > 300){
i.center.y = 300;
i.velocity = scale(i.velocity, -1);
}
}
}
// Demo
c1 = circle(Vec2(100, 100), 20);Links:
- Original:
1,
2
demo 1,
2,
source code 1 (20.6 kb),
2 (20.8 kb)
- Mine:
demo,
source code (12.1 kb)
Chapter 20: Linear impulses
Linear impulses (pushes) can help us create realistic collision responses according to the shapes' velocity, mass, fricion and restitution.
- Restitution (bounciness) represents how much energy is conserved after a collision (0: no elasticity - 1: perfect elastic).
- Friction (slidyness) will be used later in tangential collision responses (0: frictionless - 1: maximum friction).
In this chapter, the default values (friction = 0, restitution = 1) are used, and the masses are ignored.
Also, the update method now handles all three kinds of collisions, and the gravity is temporarily disabled.
The red coloring on collisions is also disabled.
// Shapes
circle = (center, radius, mass = 1, friction = 0, restitution = 1, angle = 0, velocity = Vec2(0, 0), color = "#888") => {
shape = {
type: "circle",
center: center,
radius: radius,
mass: mass,
invMass: 1 / mass,
friction: friction,
restitution: restitution,
velocity: velocity,
// (...)
}
rectangle = (center, width, height, mass = 1, friction = 0, restitution = 1, angle = 0, velocity = Vec2(0, 0), color = "#888") => {
shape = {
type: "rectangle",
center: center,
width: width,
height: height,
mass: mass,
invMass: 1 / mass,
friction: friction,
restitution: restitution,
velocity: velocity,
// (...)
};
// Correct positioning
positionalCorrection = (shape1, shape2, manifold) => {
// todo
}
// Resolve collision
resolveCollision = (shape1, shape2, manifold) => {
var relativeVelocityAlongNormal = dot(sub(shape2.velocity, shape1.velocity), manifold.normal);
if(relativeVelocityAlongNormal > 0) return; // shapes are already going away from each other
var e = 1; // total elasticity (currently 100%)
var j = -(1 + e) * relativeVelocityAlongNormal; // impulse magnitude
var impulseVector = scale(manifold.normal, j);
shape1.velocity = add(shape1.velocity, scale(impulseVector, -.5));
shape2.velocity = add(shape2.velocity, scale(impulseVector, .5));
}
// Update the physics engine
update = () => {
var push, manifold, shape1, shape2, direction, distance;
// Reset manifolds
manifolds = [];
// Reset shapes colors
for(var i of shapes){
i.color = "#888";
}
// Consider all pairs of shapes
for(var i = 0; i < shapes.length; i++){
for(var j = i; j < shapes.length; j++){
if(i != j){
shape1 = shapes[i];
shape2 = shapes[j];
// Reset manifold
manifold = null;
// Detect circle-circle collisions
if(shape1.type == "circle" && shape2.type == "circle"){
direction = sub(shape2.center, shape1.center);
distance = dist(shape1.center, shape2.center);
if(distance < (shape1.radius + shape2.radius)){
manifold = {
depth: (shape1.radius + shape2.radius) - distance,
normal: normalize(direction),
contactPoint: add(shape1.center, scale(normalize(direction), shape1.radius))
};
}
}
// Detect rectangle-rectangle collisions
else if(shape1.type == "rectangle" && shape2.type == "rectangle"){
manifold = rectangleRectangleCollision(shape1, shape2);
}
// Detect circle-rectangle collisions
else if(shape1.type == "rectangle" && shape2.type == "circle"){
tmp = shape1; shape1 = shape2; shape2 = tmp;
manifold = circleRectangleCollision(shape1, shape2);
}
else if(shape1.type == "circle" && shape2.type == "rectangle"){
manifold = circleRectangleCollision(shape1, shape2);
}
// Collision response
if(manifold){
//shape1.color = "red";
//shape2.color = "red";
push = scale(manifold.normal, manifold.depth * 0.5);
positionalCorrection(shape1, shape2, manifold);
resolveCollision(shape1, shape2, manifold);
manifolds.push(manifold);
}
}
}
}
for(i of shapes){
// Apply gravity
//i.forceAccumulator = add(i.forceAccumulator, gravity);
// Integration
integrate(i);
}
}
// Demo
c1 = circle(Vec2(190, 100), 20, 1, 0, 1, 0, Vec2(1, 1));
c2 = circle(Vec2(320, 30), 20, 1, 0, 1, 0, Vec2(-2, 2));
r1 = rectangle(Vec2(200, 220), 100, 20);
r2 = rectangle(Vec2(200, 280), 50, 50, 1, 0, 1, 0, Vec2(0, -1));Links:
- Original:
video 1,
2
3
4
demo 1,
2,
3,
4,
source code 1 (22.2 kb),
2 (22.2 kb),
3 (22.4 kb),
4 (22.8 kb)
- Mine:
demo,
source code (14.8 kb)
Chapter 21: weight
As we saw earlier, objects react to impulses proportionally to their inverse masses.
Fixed objects (also called kinematic or immovable) have an infinite mass and an invMass equal to 0, hence no reaction to impulses.
For simplicity, the shapes constructors will consider "mass = 0" as infinite mass.
The demo is updated to include light, heavy and fixed shapes.
// Shapes
circle = (center, radius, mass = 1, friction = 0, restitution = 1, angle = 0, velocity = Vec2(0, 0), color = "#888") => {
shape = {
type: "circle",
center: center,
radius: radius,
mass: mass,
invMass: mass == 0 ? 0 : 1 / mass,
// (...)
rectangle = (center, width, height, mass = 1, friction = 0, restitution = 1, angle = 0, velocity = Vec2(0, 0), color = "#888") => {
shape = {
type: "rectangle",
center: center,
width: width,
height: height,
mass: mass,
invMass: mass == 0 ? 0 : 1 / mass,
// (...)
};
// Resolve collision
resolveCollision = (shape1, shape2, manifold) => {
var relativeVelocityAlongNormal = dot(sub(shape2.velocity, shape1.velocity), manifold.normal);
if(relativeVelocityAlongNormal > 0) return; // shapes are already going away from each other
var e = 1; // total elasticity
var invMassSum = shape1.invMass + shape2.invMass;
var j = (-(1 + e) * relativeVelocityAlongNormal) / invMassSum; // impulse magnitude
var impulseVector = scale(manifold.normal, j);
shape1.velocity = add(shape1.velocity, scale(impulseVector, -shape1.invMass));
shape2.velocity = add(shape2.velocity, scale(impulseVector, shape2.invMass));
}
// Demo
c1 = circle(Vec2(190, 100), 20, 1, 0, 1, 0, Vec2(1, 1));
c2 = circle(Vec2(250, 120), 20, 0, 0, 1);
r1 = rectangle(Vec2(200, 220), 100, 20, .2);
r2 = rectangle(Vec2(200, 280), 50, 50, 10, 0, 1, 0, Vec2(0, -1));Links:
- Original:
video,
demo,
source code
(23.6 kb)
- Mine:
demo,
source code (14.9 kb)
Chapter 22: kinematic bodies
We can return early from collision resolution if both shapes are kinematic (if their invMass is 0).
// Resolve collision
resolveCollision = (shape1, shape2, manifold) => {
var relativeVelocityAlongNormal = dot(sub(shape2.velocity, shape1.velocity), manifold.normal);
if(relativeVelocityAlongNormal > 0) return; // shapes are already going away from each other
if(shape1.invMass == 0 && shape2.invMass == 0) return; // both shapes are kinematic
// (...)
}Links:
Original:
video,
demo,
source code
(24.9 kb)
Chapter 23: Positional corrections
Here we implement positionalCorrection prevent objects from overlapping: they are instantly moved away from each other proportionally to their invMass.
The restitution (bounciness) of the shapes is included in the impulse magnitude.
Finally, the gravity is restored and a fixed ground is added to the demo.
In physics, gravity is a constant (all objects fall at the same speed).
However, our integration method makes all the forces applied to an object proportional to their inverse mass.
To compensate that, in the update method, each object will receive a gravity force proportional to its mass ((G x m) / m = G).
// Correct positioning
positionalCorrection = (shape1, shape2, manifold) => {
var correction = 0.7;
var correctionAmount = manifold.depth / (shape1.invMass + shape2.invMass) * correction;
var correctionVector = scale(manifold.normal, correctionAmount);
if(shape1.invMass > 0){
translateShape(shape1, scale(correctionVector, -shape1.invMass));
}
if(shape2.invMass > 0){
translateShape(shape2, scale(correctionVector, shape2.invMass));
}
}
// Resolve collision
resolveCollision = (shape1, shape2, manifold) => {
// (...)
var e = Math.min(shape1.restitution, shape2.restitution); // total elasticity
// (...)
}
// Update the physics engine
update = () => {
// Apply gravity
for(var i of shapes){
console.log(i.mass);
i.forceAccumulator = add(i.forceAccumulator, scale(gravity, i.mass));
}
// (...)
// Integration
for(i of shapes){
integrate(i);
}
}Links:
- Original:
video,
demo,
source code
(25.9 kb)
- Mine:
demo,
source code (15.5 kb)
Chapter 24: Inertia
Inertia represents the resistance of an object to rotational forces.
In this chapter, we add the inertia, inverseInertia and angularVelocity properties for circles and rectangles.
Like the velocity, the angular velocity is damped over time, and applied to the shape's angle during integration.
Contrary to velocity, angularVelocity is a Number (because the angle is a Number too).
The inertia is a constant computed in each shape's constructor:
- Circles inertia is equal to (mass * radius²) / 2.
- Rectangles inertia is equal to (mass * (width² + height²)) / 12.
- Other polygons' inertia is detailed in the original code but not used here.
The shapes now have all they need to rotate naturally after a collision, and the next two chapters will implement that.
// Shapes
circle = (
center,
radius,
mass = 1,
friction = 0,
restitution = 1,
angle = 0,
velocity = Vec2(0, 0),
angularVelocity = 0,
color = "#888"
) => {
var inertia = (mass * (radius ** 2)) / 2;
shape = {
type: "circle",
center: center,
radius: radius,
mass: mass,
invMass: mass == 0 ? 0 : 1 / mass,
friction: friction,
restitution: restitution,
angle: angle,
velocity: velocity,
angularVelocity: angularVelocity,
inertia: inertia,
invInertia: inertia == 0 ? 0 : 1 / inertia,
forceAccumulator: Vec2(0, 0),
color: color
};
shapes.push(shape);
return shape;
}
rectangle = (
center,
width,
height,
mass = 1,
friction = 0,
restitution = 1,
angle = 0,
velocity = Vec2(0, 0),
angularVelocity = 0,
color = "#888"
) => {
var inertia = (mass * ((width ** 2) + (height ** 2))) / 12;
shape = {
type: "rectangle",
center: center,
width: width,
height: height,
mass: mass,
invMass: mass == 0 ? 0 : 1 / mass,
friction: friction,
restitution: restitution,
angle: angle,
velocity: velocity,
angularVelocity: angularVelocity,
inertia: inertia,
invInertia: inertia == 0 ? 0 : 1 / inertia,
forceAccumulator: Vec2(0, 0),
color: color,
// Rectangle vertices
vertices: [
Vec2(center.x - width / 2, center.y - height / 2), // top left
Vec2(center.x + width / 2, center.y - height / 2), // top right
Vec2(center.x + width / 2, center.y + height / 2), // bottom left
Vec2(center.x - width / 2, center.y + height / 2) // bottom right
]
};
// Rotation
if(angle) {
rotateShape(shape, angle);
}
// Normals
calcNormals(shape);
shapes.push(shape);
return shape;
};
// Shape integration
integrate = (shape) => {
// compute acceleration
var acceleration = scale(shape.forceAccumulator, shape.invMass);
// apply acceleration to velocity
shape.velocity = add(shape.velocity, acceleration);
// apply velocity to position
translateShape(shape, shape.velocity);
// apply angular velocity to angle
rotateShape(shape, shape.angularVelocity * 1);
// reset force accumulator
shape.forceAccumulator = Vec2(0, 0);
// velocity damping
shape.velocity = scale(shape.velocity, .99);
// angular velocity damping
shape.angularVelocity *= 0.99;
}
// Demo
rectangle(Vec2(350, 350), 300, 20, 0, 0.5, .9, 0.2);
circle(Vec2(190, 100), 30, 10, 1, .1);
circle(Vec2(290, 100), 30, 10, .1, .1);
circle(Vec2(390, 100), 30, 10, .01, .1);
rectangle(Vec2(500, 100), 100, 50, 10, 1, .1);
rectangle(Vec2(290, -700), 100, 50, 10, .01, .1);Links:
- Original:
video,
demo,
source code
(27.0 kb)
- Mine:
demo (without rotation),
source code (16.1 kb)
Chapter 25: Rotational impulses
Just like position has velocity and acceleration, angle has angular velocity and torque (angular acceleration).
Angular impulses can affect an object's torque every time a force is not applied towards its center of gravity.
A cross function is added, to compute a "cross-product" (-ish) between two 2D vectors.
It returns a value between -1 and 1 representing the angle between two vectors (from 1: parallel, to 0: perpendicular, to -1: opposed).
The resolveCollision method is rewritten below to allow rectangles to rotate after a collision.
Circles are not affected by this code because the can only rotate after tangential impulses, caused by friction. Chapter 26 will cover this.
cross = (v, w) => v.x * w.y - v.y * w.x;
// Resolve collision
resolveCollision = (shape1, shape2, manifold) => {
// If both objects are kinematic, skip
if(shape1.invMass == 0 && shape2.invMass == 0) return;
// Vectors from each object's center to the contact point
var penetrationToCentroidA = sub(manifold.contactPoint, shape1.center);
var penetrationToCentroidB = sub(manifold.contactPoint, shape2.center);
// Linear velocity contribution at the contact point due to angular velocity
var angularVelocityPenetrationCentroidA = Vec2(
-shape1.angularVelocity * penetrationToCentroidA.y,
shape1.angularVelocity * penetrationToCentroidA.x
);
var angularVelocityPenetrationCentroidB = Vec2(
-shape2.angularVelocity * penetrationToCentroidB.y,
shape2.angularVelocity * penetrationToCentroidB.x
);
// Total velocity at the contact point = linear + rotational
var relativeVelocityA = add(shape1.velocity, angularVelocityPenetrationCentroidA);
var relativeVelocityB = add(shape2.velocity, angularVelocityPenetrationCentroidB);
// Relative velocity between both contact points
var relativeVel = sub(relativeVelocityB, relativeVelocityA);
// Project relative velocity onto the collision normal
var velocityInNormal = dot(relativeVel, manifold.normal);
// If the objects are moving apart (positive relative velocity along the normal), skip
if(velocityInNormal > 0) return;
// Restitution coefficient (bounciness)
var e = Math.min(shape1.restitution, shape2.restitution);
// Compute the "lever arm" cross product (how far from the center the impulse acts)
var pToCentroidCrossNormalA = cross(penetrationToCentroidA, manifold.normal);
var pToCentroidCrossNormalB = cross(penetrationToCentroidB, manifold.normal);
// Effective inverse mass including both linear and rotational contributions
var invMassSum = shape1.invMass + shape2.invMass;
var rigiAInvInertia = shape1.invInertia;
var rigiBInvInertia = shape2.invInertia;
var crossNSum =
pToCentroidCrossNormalA * pToCentroidCrossNormalA * rigiAInvInertia +
pToCentroidCrossNormalB * pToCentroidCrossNormalB * rigiBInvInertia;
// Compute the scalar impulse magnitude (j)
var j = -(1 + e) * velocityInNormal;
j /= (invMassSum + crossNSum);
// Convert scalar impulse into a vector along the collision normal
var impulseVector = scale(manifold.normal, j);
// Apply impulse to linear velocities (in opposite directions)
shape1.velocity = sub(shape1.velocity, scale(impulseVector, shape1.invMass));
shape2.velocity = add(shape2.velocity, scale(impulseVector, shape2.invMass));
// Apply rotational impulse based on lever arm and inverse inertia
shape1.angularVelocity += -pToCentroidCrossNormalA * j * rigiAInvInertia;
shape2.angularVelocity += pToCentroidCrossNormalB * j * rigiBInvInertia;
}Links:
Original:
video 1,
2,
3,
4,
5,
demo 1,
2,
source code 1 (29.6kb)
2
(29.5 kb)
- Mine:
demo,
source code (18.2 kb)
Chapter 26: Frictional impulses
The last step needed to make balls roll on a slope or after a collision, is to implement friction.
// Resolve collision
resolveCollision = (shape1, shape2, manifold) => {
// If both objects are kinematic, skip
if(shape1.invMass == 0 && shape2.invMass == 0) return;
// Normal impulse
// (...)
// Frictional impulse
// Compute the component of the relative velocity along the collision normal
var velocityInNormalDirection = scale(manifold.normal, dot(relativeVel, manifold.normal));
// Subtract that from the total relative velocity to get the tangential direction
var tangent = sub(relativeVel, velocityInNormalDirection);
// Reverse tangent direction (optional, depending on sign convention)
tangent = scale(tangent, -1);
// Use the smallest friction coefficient between the two shapes
var minFriction = Math.min(shape1.friction, shape2.friction);
// Compute lever arms (distance vectors crossed with tangent direction)
// Used to determine rotational influence for each body
var pToCentroidCrossTangentA = cross(penetrationToCentroidA, tangent);
var pToCentroidCrossTangentB = cross(penetrationToCentroidB, tangent);
// Effective inverse mass for the tangential direction (accounts for rotation)
var crossSumTangent =
pToCentroidCrossTangentA * pToCentroidCrossTangentA * rigiAInvInertia +
pToCentroidCrossTangentB * pToCentroidCrossTangentB * rigiBInvInertia;
// Compute the tangential (frictional) impulse magnitude
// This resists sliding motion along the tangent direction
// Original tuto used the formula -(1+e) * dot(...) but it makes no sense to use (1+e) here
var frictionalImpulse = -dot(relativeVel, tangent) * minFriction;
// Divide by total effective mass (linear + rotational)
frictionalImpulse /= (invMassSum + crossSumTangent);
// Limit frictional impulse so it doesn’t exceed the normal impulse
if(frictionalImpulse > j){ frictionalImpulse = j; }
// Convert scalar friction impulse into a vector along the tangent
var frictionalImpulseVector = scale(tangent, frictionalImpulse);
// Apply friction impulse to linear velocities of both bodies
shape1.velocity = sub(shape1.velocity, scale(frictionalImpulseVector, shape1.invMass));
shape2.velocity = add(shape2.velocity, scale(frictionalImpulseVector, shape2.invMass));
// Apply angular (rotational) impulse due to friction
shape1.angularVelocity += -pToCentroidCrossTangentA * frictionalImpulse * rigiAInvInertia;
shape2.angularVelocity += pToCentroidCrossTangentB * frictionalImpulse * rigiBInvInertia;
}A little warning here: when I showed this code to ChatGPT, it suggested a few modifications (to take with a pinch of salt):
- "(1+e) * " has no physical sense in friction. We should do this instead:
var frictionalImpulse = -dot(relativeVel, tangent) * minFriction;- Coulomb friction must be clamped:
if (Math.abs(frictionalImpulse) > j * minFriction)
frictionalImpulse = j * minFriction * Math.sign(frictionalImpulse);We will consider these ideas later.
Links:
- Original:
video 1,
2,
3,
demo 1,
2,
source code 1 (33.6 kb),
2
(36.1 kb)
- Mine:
demo,
source code (20.4 kb)
We are now at the same level as my 2019 library mini2Dphysics. The next chapters will finally cover the last features that interest me.
Chapter 27: Anchor points
To start implementing joints between rigid bodies, we need a way to define anchor points.
These anchor points are defined relatively to a shape's center, and are recomputed in world coordinates when the shape is rotated or translated.
For debug purposes, they are drawn in green.
// Shapes
circle = ( /* ... */ ) => {
var shape = {
// (...)
color: color,
anchorPoints: []
};
shapes.push(shape);
return shape;
}
rectangle = ( /* ... */ ) => {
var shape = {
// (...)
color: color,
anchorPoints: [],
// (...)
};
};
// Add anchor point
// (anchor is in local coordinates)
addAnchor = (anchor, shape) => {
var anchor = add(anchor, shape.center);
shape.anchorPoints.push(anchor);
return shape.anchorPoints.length - 1;
}
// Translate a shape
translateShape = (shape, offset) => {
// (...)
// Move anchor points
for(var i in shape.anchorPoints){
shape.anchorPoints[i] = add(shape.anchorPoints[i], offset);
}
}
// Rotate a shape around its center (angle in radians)
rotateShape = (shape, angle) => {
// (...)
// Rotate anchor points
for(var i in shape.anchorPoints){
shape.anchorPoints[i] = rotate(shape.anchorPoints[i], shape.center, angle);
}
}
// Render the scene
draw = () => {
// Reset canvas
a.width = a.width;
// Draw shapes
for(var i of shapes){
// (...)
// Debug: draw anchor points
for(var j of i.anchorPoints){
drawPoint(j, 5, "green");
}
}
// (...)
}
// Demo
rectangle(Vec2(350, 350), 300, 20, 0, 0.5, .9, 0.2);
circle(Vec2(190, 100), 30, 10, 1, .1);
c1 = circle(Vec2(290, 100), 30, 10, .1, .1);
circle(Vec2(390, 100), 30, 10, .01, .1);
rectangle(Vec2(500, 100), 100, 50, 10, 1, .1);
r1 = rectangle(Vec2(290, -700), 100, 50, 10, .01, .1);
addAnchor(Vec2(15, 15), c1);
addAnchor(Vec2(-30, 15), r1);Links:
- Original:
video,
demo,
source code
(37.2 kb)
- Mine:
demo,
source code (21.1 kb)
Chapter 28: Apply a force outside the center
Anchor points are used to apply forces on objects. When the anchor is not on the center of a shape, the force provokes a linear and a rotational motion.
A torqueAccumulator (Number) is added to the shapes constructors, and corresponds to a rotational acceleration.
It's important to note here that impulses and forces are different: impulses are used to instantly modify a velocity, while forces are used to instantly modify an acceleration.
It's possible to replace forces by impulses proportional to deltaT (the time between two frames), but we'll see that later.
Here, mouse inputs are used to apply forces to any shape.
An isPointInside function is created to check if a shape is clicked.
The integrate method is completed too.
// Globals
selectedRigidBody = null;
selectedPosition = null;
selectedAnchorId = null;
// Is point inside a shape
isPointInside = (point, shape) => {
// Circle
if(shape.type == "circle"){
var distanceToCenter = len(sub(shape.center, point));
return shape.radius > distanceToCenter;
}
// Rectangle
else {
var isInside = false;
for(var i = 0; i < shape.vertices.length; i++){
var vertex = shape.vertices[i];
var normal = shape.normals[i];
var vertToPoint = sub(point, vertex);
var d = dot(vertToPoint, normal);
if(d > 0) return false;
else isInside = true;
}
return isInside;
}
}
// Add force on a point
// (point is in world coordinates)
addForceAtPoint = (point, shape, force) => {
var direction = sub(point, shape.center);
shape.forceAccumulator = add(shape.forceAccumulator, force);
shape.torqueAccumulator += cross(direction, force);
}
// Shape integration
integrate = (shape) => {
// compute acceleration and rotational acceleration
var acceleration = scale(shape.forceAccumulator, shape.invMass);
var rotationalAcceleration = shape.torqueAccumulator * shape.invInertia;
// apply acceleration to velocity
shape.velocity = add(shape.velocity, acceleration);
// apply velocity to position
translateShape(shape, shape.velocity);
// apply rotational acceleration to angular velocity
shape.angularVelocity += rotationalAcceleration * 1;
// apply angular velocity to angle
rotateShape(shape, shape.angularVelocity * 1);
// velocity damping
shape.velocity = scale(shape.velocity, .99);
// angular velocity damping
shape.angularVelocity *= 0.99;
// reset force accumulator
shape.forceAccumulator = Vec2(0, 0);
// reset torque accumulator
shape.torqueAccumulator = 0;
}
// Mouse interactions
handleMouseObjectInteraction = () => {
var mousePos = Vec2(mx, my);
// Left button pressed
if(mlb){
for(var i = 0; i < shapes.length; i++){
var mouseInside = isPointInside(mousePos, shapes[i]);
if(mouseInside && selectedRigidBody == null){
selectedRigidBody = shapes[i];
selectedPosition = copy(mousePos);
var localPos = sub(mousePos, shapes[i].center);
addAnchor(localPos, shapes[i]);
selectedAnchorId = shapes[i].anchorPoints.length - 1;
}
}
}
// Left button released
else {
if(selectedRigidBody != null){
selectedRigidBody.anchorPoints.pop();
selectedRigidBody = null;
}
selectedAnchorId = null;
selectedPosition = null;
}
// Apply force
if(selectedRigidBody && selectedPosition){
var start = selectedRigidBody.anchorPoints[selectedAnchorId];
var force = sub(mousePos, start);
addForceAtPoint(start, selectedRigidBody, scale(force, 0.01));
}
}
// Update the physics engine
update = () => {
// (...)
// Mouse interactions
handleMouseObjectInteraction();
}
// Demo
rectangle(Vec2(350, 350), 400, 20, 0, 0.5, .9); // not tilted
Links:
- Original:
video 1,
2,
demo,
source code
(39.6 kb)
- Mine:
demo,
source code (23.3 kb)
Chapter 29: Force joints
With anchor points that can apply forces, we can now implement joints.
The simplest kind of joint, the force joint, attracts two anchor points with a defined strength.
A forceJoint constructor and a handleJoints are created.
// Globals
joints = [];
// Update the physics engine
update = () => {
// (...)
// joints
handleJoints();
}
// Render the scene
draw = () => {
// (...)
// Debug: draw joints
for(var i of joints){
drawLine(i.rigiA.anchorPoints[i.anchorA], i.rigiB.anchorPoints[i.anchorB], "orange");
}
}
// Joints
// Force joint
forceJoint = (rigiA, anchorA, rigiB, anchorB, strength) => {
var joint = {
type: "force",
rigiA: rigiA,
anchorA: anchorA,
rigiB: rigiB,
anchorB: anchorB,
strength: strength
};
joints.push(joint);
return joint;
}
// Joint handler
handleJoints = () => {
for(var i = 0; i < joints.length; i++){
var joint = joints[i];
var forceHalving = (joint.rigiA.invMass == 0 || joint.rigiB.invMass == 0) ? 1 : 0.5;
var anchorAPos = joint.rigiA.anchorPoints[joint.anchorA];
var anchorBPos = joint.rigiB.anchorPoints[joint.anchorB];
var direction = sub(anchorBPos, anchorAPos);
// Force joint
if(joint.type == "force"){
// Update connection A
addForceAtPoint(anchorBPos, joint.rigiA, scale(direction, joint.strength * forceHalving));
// Update connection B
addForceAtPoint(anchorAPos, joint.rigiB, scale(direction, -joint.strength * forceHalving));
}
}
}
// Demo
rectangle(Vec2(350, 550), 500, 20, 0, 0.5, .9);
r1 = rectangle(Vec2(200, 200), 200, 100, 100);
a1 = addAnchor(Vec2(50,25), r1);
c1 = circle(Vec2(500, 100), 60, 100);
a2 = addAnchor(Vec2(-60,0), c1);
j1 = forceJoint(r1, a1, c1, a2, .1);Links:
- Original:
video,
demo,
source code
(41.9 kb)
- Mine:
demo,
source code (24.4 kb)
Chapter 30: Spring joints
Spring joints simulate realistic springs behavior, with oscillatory movement and proportional force:
The force is equal to the inverse of the spring displacement (from its rest length) times the spring's stiffness constant (according to the simplified Hook's law: F = -x * k).
// Spring joint
springJoint = (rigiA, anchorA, rigiB, anchorB, stiffness, restLength) => {
var joint = {
type: "spring",
rigiA: rigiA,
anchorA: anchorA,
rigiB: rigiB,
anchorB: anchorB,
stiffness: stiffness,
restLength: restLength
};
joints.push(joint);
return joint;
}
// Joint handler
handleJoints = () => {
for(var i = 0; i < joints.length; i++){
var joint = joints[i];
var forceHalving = (joint.rigiA.invMass == 0 || joint.rigiB.invMass == 0) ? 1 : 0.5;
var anchorAPos = joint.rigiA.anchorPoints[joint.anchorA];
var anchorBPos = joint.rigiB.anchorPoints[joint.anchorB];
var direction = sub(anchorBPos, anchorAPos);
var distance = len(direction);
// Force joint
if(joint.type == "force"){
// Update connection A
addForceAtPoint(anchorBPos, joint.rigiA, scale(direction, joint.strength * forceHalving));
// Update connection B
addForceAtPoint(anchorAPos, joint.rigiB, scale(direction, -joint.strength * forceHalving));
}
// Spring joint
else if(joint.type == "spring"){
var restDistance = distance - joint.restLength;
var forceMagnitude = restDistance * joint.restLength * joint.stiffness * forceHalving;
var force = scale(normalize(direction), forceMagnitude);
// Update connection A
if(joint.rigiA.invMass != 0){
addForceAtPoint(anchorAPos, joint.rigiA, force);
}
// Update connection B
if(joint.rigiB.invMass != 0){
addForceAtPoint(anchorBPos, joint.rigiB, scale(force, -1));
}
}
}
}
// Demo
j1 = springJoint(r1, a1, c1, a2, .005, 50);Links:
- Original:
video,
demo,
source code
(43.6 kb)
- Mine:
demo,
source code (25.3 kb)
Chapter 31: Reverse force joints
Reverse force joints are used to create a repulsion and maintaining a minimum distance between two objects.
They introduce the concept of distance-based force activation.
They have no attractive or repulsive effect when the distance is bigger than the minimum effect distance.
// Joint handler
handleJoints = () => {
for(var i = 0; i < joints.length; i++){
// (...)
// Reverse force joint
else if(joint.type == "reverseForce"){
var forceMagnitude = Math.max(0, joint.maxEffectDistance - distance);
// Update connection A
if(joint.rigiA.invMass != 0){
addForceAtPoint(anchorBPos, joint.rigiA, scale(normalize(direction), -forceMagnitude * joint.strength * forceHalving));
}
// Update connection B
if(joint.rigiB.invMass != 0){
addForceAtPoint(anchorAPos, joint.rigiB, scale(normalize(direction), forceMagnitude * joint.strength * forceHalving));
}
}
}
}
// Demo
j1 = reverseForceJoint(r1, a1, c1, a2, .05, 200);Links:
- Original:
video,
demo,
source code
(45.3 kb)
- Mine:
demo,
source code (26.2 kb)
Chapter 32: Control which objects can collide with each other
For now we simply add a noCollision array in each shape's constructor, and we will use it in the next two chapters.
Links:
Original:
video,
demo,
source code
(46.0 kb)
Chapter 33: Fixed joints
Fixed joints and hinge joints (that we will see in next chapter) are the main reasons that made me follow this tutorial from scratch. Fixed joints are particularly important because they allow to create compound shapes.
Sadly, the original demo, source code and video didn't fulfill their mission: they correctly introduce the iterative approach (to fix the shapes' position and angle many times per frame) and disable collisions between jointed shapes, but the joint they implement is not firm enough: the shapes wobble!
Unable to fix it myself, I had ChatGPT fix it for me and explain to me what was wrong:
The angle correction's force was too weak, and applied using angularVelocity tweaks instead of impulses.
The fixed code below adds direct angle projection at each iteration for a more precise result.
// Shapes
circle = (/* ... */) => {
// (...)
anchorPoints: [],
noCollision: [],
}
rectangle = (/* ... */) => {
// (...)
anchorPoints: [],
noCollision: [],
}
// Update the physics engine
update = () => {
var push, manifold, shape1, shape2, direction, distance, i, j;
// Reset manifolds
manifolds = [];
// Reset shapes colors, apply gravity
for(i of shapes){
i.color = "#888";
i.forceAccumulator = add(i.forceAccumulator, scale(gravity, i.mass));
}
// Consider all pairs of shapes
for(i = 0; i < shapes.length; i++){
for(j = i; j < shapes.length; j++){
shape1 = shapes[i];
shape2 = shapes[j];
// Ignore self-collisions, pairs of immobile shapes and collisions in fixed joints
if(i != j && !(shape1.invMass == 0 && shape2.invMass == 0) && !shape1.noCollision.includes(j)){
// (...)
}
}
}
// Joints (must be enforced before integration)
handleJoints();
// Integration
for(i of shapes){
integrate(i);
}
// Mouse interactions
handleMouseObjectInteraction();
}
// Render the scene
draw = () => {
// (...)
// Debug: draw manifolds
for(var i of manifolds){
drawPoint(i.contactPoint, 5, "#04F");
//drawLine(i.contactPoint, add(i.contactPoint, scale(i.normal, 50)), "#04F");
}
// (...)
}
// Fixed joint
fixedJoint = (rigiA, anchorA, rigiB, anchorB, iterations = 20) => {
var joint = {
type: "fixed",
rigiA: rigiA,
anchorA: anchorA,
rigiB: rigiB,
anchorB: anchorB,
iterations: iterations,
rigiABounce: rigiA.restitution,
rigiBBounce: rigiB.restitution,
rigiAFriction: rigiA.friction,
rigiBFriction: rigiB.friction,
initialLength: len(sub(rigiA.anchorPoints[anchorA], rigiB.anchorPoints[anchorB])),
relativeAngle: rigiB.angle - rigiA.angle
};
rigiA.noCollision.push(shapes.indexOf(rigiB));
rigiB.noCollision.push(shapes.indexOf(rigiA));
joints.push(joint);
return joint;
}
// Enable/disable friction and restitution in fixed/hinge joints
setMaterialZero = joint => {
joint.rigiA.restitution = 0;
joint.rigiA.friction = 0;
joint.rigiB.restitution = 0;
joint.rigiB.friction = 0;
}
restoreMaterial = joint => {
joint.rigiA.restitution = joint.rigiABounce;
joint.rigiA.friction = joint.rigiAFriction;
joint.rigiB.restitution = joint.rigiBBounce;
joint.rigiB.friction = joint.rigiBFriction;
}
// Joint handler
handleJoints = () => {
var joint, forceHalving, anchorAPos, anchorBPos, direction, distance, restDistance, forceMagnitude, force, normal, contact, currentOrientationDiff, fixedOrientationVel, angleError, stiffness, avgAngVel, i, j;
for(i = 0; i < joints.length; i++){
joint = joints[i];
forceHalving = (joint.rigiA.invMass == 0 || joint.rigiB.invMass == 0) ? 1 : 0.5;
anchorAPos = joint.rigiA.anchorPoints[joint.anchorA];
anchorBPos = joint.rigiB.anchorPoints[joint.anchorB];
direction = sub(anchorBPos, anchorAPos);
distance = len(direction);
// Force joint
if(joint.type == "force"){
// (...)
}
// Spring joint
else if(joint.type == "spring"){
// (...)
}
// Reverse force joint
else if(joint.type == "reverseForce"){
// (...)
}
// Fixed joint
else if(joint.type == "fixed"){
setMaterialZero(joint);
// Move shapes in order to make the anchor points superposed, proportionally to their inverse masses
delta = sub(anchorBPos, anchorAPos);
totalInvMass = joint.rigiA.invMass + joint.rigiB.invMass;
if(totalInvMass > 0){
correctionA = scale(delta, joint.rigiA.invMass / totalInvMass);
correctionB = scale(delta, joint.rigiB.invMass / totalInvMass);
// Move A and B
translateShape(joint.rigiA, correctionA);
translateShape(joint.rigiB, scale(correctionB, -1));
}
// Update connection A
for(j = 0; j < joint.iterations; j++){
direction = sub(anchorBPos, anchorAPos);
distance = len(direction);
if(distance < 0.00001) break;
normal = copy(normalize(direction));
contact = {
depth: 0,
normal: normal,
contactPoint: anchorBPos,
rigiA: joint.rigiB,
rigiB: joint.rigiA
};
if(distance > joint.initialLength){
contact.depth = distance - joint.initialLength;
}
else {
contact.depth = joint.initialLength - distance;
contact.normal = scale(contact.normal, -1);
}
positionalCorrection(joint.rigiA, joint.rigiB, contact);
resolveCollision(joint.rigiA, joint.rigiB, contact);
}
// Fix orientation strongly
currentOrientationDiff = joint.rigiB.angle - joint.rigiA.angle - 0.01;
angleError = joint.relativeAngle - currentOrientationDiff;
// Apply symmetric angular correction
stiffness = 1; // try 1.0 for absolutely rigid
joint.rigiA.angle -= angleError * stiffness * 0.5;
joint.rigiB.angle += angleError * stiffness * 0.5;
// Update connection B
for(j = 0; j < joint.iterations; j++){
direction = sub(anchorBPos, anchorAPos);
distance = len(direction);
if(distance < 0.00001) break;
normal = copy(normalize(direction));
contact = {
depth: 0,
normal: normal,
contactPoint: anchorBPos,
rigiA: joint.rigiA,
rigiB: joint.rigiB
};
if(distance > joint.initialLength){
contact.depth = distance - joint.initialLength;
}
else{
contact.depth = joint.initialLength - distance;
contact.normal = scale(contact.normal, -1);
}
positionalCorrection(joint.rigiB, joint.rigiA, contact);
resolveCollision(joint.rigiB, joint.rigiA, contact);
}
// Fix orientation strongly
currentOrientationDiff = joint.rigiA.angle - joint.rigiB.angle;
angleError = joint.relativeAngle - currentOrientationDiff;
stiffness = 1;
joint.rigiA.angle += angleError * stiffness * 0.5;
joint.rigiB.angle -= angleError * stiffness * 0.5;
avgAngVel = (joint.rigiA.angularVelocity + joint.rigiB.angularVelocity) * 0.5;
joint.rigiA.angularVelocity = avgAngVel;
joint.rigiB.angularVelocity = avgAngVel;
restoreMaterial(joint);
}
}
}
// Demo
for(i = 0; i < 40; i++){
circle(Vec2(i*20, -i*20-500), 10, 10);
}
rectangle(Vec2(380, 450), 600, 20, 0, 0.5, .9);
r1 = rectangle(Vec2(300, 200), 200, 100, 100);
a1 = addAnchor(Vec2(75, 0), r1);
r2 = rectangle(Vec2(600, 200), 300, 25, 100);
a2 = addAnchor(Vec2(-125, 0), r2);
c1 = circle(Vec2(300, 320), 60, 100);
j1 = fixedJoint(r1, a1, r2, a2);Links:
- Original:
video,
demo,
source code
(53.3 kb)
- Mine:
demo,
source code (30.9 kb)
Chapter 34: Hinge joints
Hinge joints are almost identical to fixed joints (they also have iterative solving, collision disabling and strong positional solving), but differ in terms of angles: the shapes are attached firmly together but they rotate freely.
// Hinge joint
hingeJoint = (rigiA, anchorA, rigiB, anchorB, iterations = 20) => {
var joint = {
type: "hinge",
rigiA: rigiA,
anchorA: anchorA,
rigiB: rigiB,
anchorB: anchorB,
iterations: iterations,
rigiABounce: rigiA.restitution,
rigiBBounce: rigiB.restitution,
rigiAFriction: rigiA.friction,
rigiBFriction: rigiB.friction,
initialLength: len(sub(rigiA.anchorPoints[anchorA], rigiB.anchorPoints[anchorB])),
};
rigiA.noCollision.push(shapes.indexOf(rigiB));
rigiB.noCollision.push(shapes.indexOf(rigiA));
joints.push(joint);
return joint;
}
// Update the physics engine
update = () => {
// (...)
// Ignore self-collisions, pairs of immobile shapes and collisions in fixed/hinge joints
if(
i != j && !(shape1.invMass == 0 && shape2.invMass == 0) && !shape1.noCollision.includes(j)
){
// (...)
}
}
}
// (...)
}
// Joint handler
handleJoints = () => {
// (...)
for(i = 0; i < joints.length; i++){
// (...)
// Hinge joint
else if(joint.type == "hinge"){
setMaterialZero(joint);
// Move shapes in order to make the anchor points superposed, proportionally to their inverse masses
var delta = sub(anchorBPos, anchorAPos);
var totalInvMass = joint.rigiA.invMass + joint.rigiB.invMass;
if(totalInvMass > 0){
correctionA = scale(delta, joint.rigiA.invMass / totalInvMass);
correctionB = scale(delta, joint.rigiB.invMass / totalInvMass);
// Move A and B
translateShape(joint.rigiA, correctionA);
translateShape(joint.rigiB, scale(correctionB, -1));
}
// Update connection A
for(var j = 0; j < joint.iterations; j++){
direction = sub(anchorBPos, anchorAPos);
distance = len(direction);
if(distance < 0.00001) break;
normal = copy(normalize(direction));
contact = {
depth: 0,
normal: normal,
contactPoint: anchorBPos,
rigiA: joint.rigiB,
rigiB: joint.rigiA
};
if(distance > joint.initialLength){
contact.depth = distance - joint.initialLength;
}
else {
contact.depth = joint.initialLength - distance;
contact.normal = scale(contact.normal, -1);
}
positionalCorrection(joint.rigiA, joint.rigiB, contact);
resolveCollision(joint.rigiA, joint.rigiB, contact);
}
// Update connection B
for(j = 0; j < joint.iterations; j++){
direction = sub(anchorBPos, anchorAPos);
distance = len(direction);
if(distance < 0.00001) break;
normal = copy(normalize(direction));
contact = {
depth: 0,
normal: normal,
contactPoint: anchorBPos,
rigiA: joint.rigiA,
rigiB: joint.rigiB
};
if(distance > joint.initialLength){
contact.depth = distance - joint.initialLength;
}
else{
contact.depth = joint.initialLength - distance;
contact.normal = scale(contact.normal, -1);
}
positionalCorrection(joint.rigiB, joint.rigiA, contact);
resolveCollision(joint.rigiB, joint.rigiA, contact);
}
restoreMaterial(joint);
}
}
}
// Demo
j1 = hingeJoint(r1, a1, r2, a2);
Links:
- Original:
video,
demo (fixed),
source code (fixed)
(48.9 kb)
- Mine:
demo,
source code (33.9 kb)
Chapter 35 (bonus): Collision masks and groups
This chapter shows an advanced technique for telling which objects should and should not collide with each other. We don't need that.
Links:
Original:
video,
demo,
source code
(50.1 kb)
Chapter 36 (bonus): Collision matrix
An even more advanced collision filtering system, that we also won't use.
Links:
Original:
video,
demo,
source code
(63.1 kb)
Yayyy, I completed my dream 2D physics engine in two weeks and a little less than 34kb! It's now time to golf it!
GOLFING MY ENGINE
Phase 1: line-by-line minification and simplification
The canvas 2D context is retrieved using a template literal (implied parentheses).
2D vector functions and globals are renamed.
ES6 shorthand property names are used in V().
len2 and copy are removed.
repetitions are added in rotate for better zip compression.
null is replaced with 0.
Minified size: 579b → 395b.
// Canvas setup
var c=a.getContext`2d`,
// 2D vectors
V=(x,y)=>({x,y}), // Vec2 constructor
n=v=>S(v,1/l(v)), // normalize
l=v=>d(v,v)**.5, // length
N=v=>V(v.y,-v.x), // normal
d=(x,y)=>x.x*y.x+x.y*y.y, // dot
A=(x,y)=>V(x.x+y.x,x.y+y.y), // add
s=(x,y)=>A(x,S(y,-1)), // sub
S=(x,y)=>V(x.x*y,x.y*y), // scale
D=(x,y)=>l(s(x,y)), // dist
r=(x,y,c)=>(V((x.x-y.x)*Math.cos(c)-(x.y-y.y)*Math.sin(c)+y.x,(x.x-y.x)*Math.sin(c)+(x.y-y.y)*Math.cos(c)+y.y)), // rotate
C=(x,y)=>x.x*y.y-x.y*y.x, // cross
// Globals
m=0,p=0, // mouse position, pressed
sr=0,sp=0,sa=0, // selected rigidbody, position, anchor
H=[],J=[],M=[], // shapes, joints, manifolds
G=V(0,.1), // GravityEvent listeners are golfed using the good old "e.type[7]" trick.
e.type is either "mouseup" or "mousedown", so e.type[7] is either trueish ("w") or falseish (undefined).
Minified size: 108b → 101zb.
onmousemove=o=>m=V(o.pageX-a.offsetLeft,o.pageY-a.offsetTop),
onmousedown=onmouseup=o=>p=!!o.type[7],Circle and rectangle are replaced with a single shape constructor.
radius, width and height are replaced with size1 and size2.
angle and velocity parameters are removed.
ES6 shorthand properties are used.
attributes names are not minified (yet) to keep objects readable.
temp vars are added to the parameters instead of using var or let.
== is replaced with === to improve performances.
Minified size: 834b → 450b
// Shapes
shape=(
type,
center,
size1, // radius (circle) or width (rectangle)
size2, // height (rectangle only)
mass=1,
friction=0,
restitution=1,
color,
// inertia
inertia=(type==="circle"?mass*size1**2/2:mass*(size1**2+size2**2)/12),
// shape
s={
type,
center,
size1,
size2,
mass,
invMass:mass===0?0:1/mass,
friction,
restitution,
angle:0,
velocity:V(0,0),
angularVelocity:0,
inertia,
invInertia:n?0:1/n,
forceAccumulator:V(0,0),
torqueAccumulator:0,
color,
anchorPoints:[],
noCollision:[],
normals:[],
vertices:type==="circle"?[]:[
V(center.x-size1/2,center.y-size2/2),
V(center.x+size1/2,center.y-size2/2),
V(center.x+size1/2,center.y+size2/2),
V(center.x-size1/2,center.y+size2/2)
]
}
)=>(
cn(s), // compute normals (rectangles only)
H.push(s) // add shape in shapes list and return shape
);Functions involving points and shapes are renamed (two letters each).
vertices.length and normals.length are replaced with 4 (because we only deal with rectangles).
Temp vars are removed when possible.
Logic is improved
All the comments are rewritten.
Minified size: 1329b → 1030b.
// Check if a point is inside a shape
// params: point (world coordinates), shape
pi=(point,shape,t=1,i=4)=>{
// circles: return true if radius is bigger than distance to center
if(shape.type==="circle")t=shape.size1>l(s(shape.center,point));
// rectangles: return false if dot(sub(point,vertex),normal) > 0 for any edge
else for(;i--;)if(d(s(point,shape.vertices[i]),shape.normals[i])>0)t=0;
return t
},
// Add an anchor to a shape
// params: anchor (local coordinates), shape
anchor=(anchor,shape)=>(
// add anchor in the point's anchors list (converted in world coordinates)
shape.anchorPoints.push(A(anchor,shape.center)),
// return anchor index
shape.anchorPoints.length-1
),
// Add force on a point
// params: point (world coordinates), shape, force (2D vector)
af=(point,shape,force)=>{
// translation force
shape.forceAccumulator=A(shape.forceAccumulator,force),
// rotation force
shape.torqueAccumulator+=C(s(point,shape.center),force)
},
// Translate a shape
// params: shape, offset (2D vector)
ts=(shape,offset,n)=>{
// add offset to the shape's center
shape.center=A(shape.center,offset);
// add offset to the shape's vertices (if any)
for(n in shape.vertices)
shape.vertices[n]=A(shape.vertices[n],offset);
// add offset to the shape's anchor points
for(n in shape.anchorPoints)
shape.anchorPoints[n]=A(shape.anchorPoints[n],offset)
},
// Rotate a shape around its center
// params: shape, angle (in radians)
rs=(shape,angle,t)=>{
// update angle
shape.angle+=angle;
// rectangles
if(shape.type==="rectangle"){
// rotate rectangle vertices
for(t in shape.vertices)
shape.vertices[t]=r(shape.vertices[t],shape.center,angle);
// compute rectangle normals
cn(shape);
}
// rotate anchor points
for(t in shape.anchorPoints)
shape.anchorPoints[t]=r(shape.anchorPoints[t],shape.center,angle)
},
// Shape integration
si=shape=>{
// skip fixed objects
if(shape.invMass!==0){
// add force accumulator to velocity (proportionally to inverse mass)
shape.velocity=A(shape.velocity,S(shape.forceAccumulator,shape.invMass)),
// add velocity to position
ts(shape,shape.velocity),
// damp velocity
shape.velocity=S(shape.velocity,.99),
// reset force accumulator
shape.forceAccumulator=V(0,0),
// add torque to angular velocity (proportionally to inverse inertia)
shape.angularVelocity+=shape.torqueAccumulator*shape.invInertia,
// add angular velocity to angle
rs(shape,shape.angularVelocity),
// damp angular velocity
shape.angularVelocity*=.99,
// reset torque accumulator
shape.torqueAccumulator=0
}
},
// Compute the normals of a polygon
cn=(shape,t=0)=>{
// rectangle only
if(shape.type!=="circle"){
// compute 4 normals
for(;t<4;t++)
shape.normals[t]=(N(n(s(shape.vertices[(t+1)%4],shape.vertices[t]))))
}
},Functions dedicated to collision detection are minified similarly.
Number.MAX_VALUE is replaced by 9e9.
Minified size: 1405b → 943b.
// Detect rectangle-rectangle collisions using separating-axis theorem (SAT)
// rectangles are tested against each other's axis and we choose the minimal penetration depth
// params: rect1, rect2
rr=(rect1,rect2,e,r)=>{
// test rect2 against rect1's axis
e=cp(rect1,rect2);
// return null if no collision
if(e===null)return e;
// test rect1 against rect2's axis
r=cp(rect2,rect1);
// return null (if no collision) or the manifold with the smallest penetration depth (flip the normal if it's a rect2 axis)
return r===null?r:(
e.depth<r.depth
?e
:(r.normal=S(r.normal,-1),r)
)
},
// Get contact point
// all normals of rect1 are tested as potential separating axes
// params: rect1, rect2
cp=(t,n,r=null,e=9e9,l=null,o=0)=>{
// for each axis
for(;o<4;o++){
// if no support point found (no collision), return null
if((l=fs(t.normals[o],t.vertices[o],n.vertices))===null)return l;
// create/replace the manifold r if this axis has the smallest penetration depth
l.depth<e&&(
r={
depth:e=l.depth,
normal:t.normals[o],
contactPoint:l.vertex
}
)
}
// return the manifold that has the smallest penetration depth
return r
},
// Find a support point
// find which vertex from the other rectangle penetrates the deepest in a given axis
// params: normal, point (from rect1), vertices (from rect2)
fs=(normal,point,vertices,e=0,l=null,u=null,o=0)=>{
// for each vertex
for(;o<4;o++)
// if penetration depth is higher than max depth e, save it in u and save the support point in l
(u=d(s(vertices[o],point),S(normal,-1)))>e&&(
e=u,
l={
vertex:vertices[o],
depth:u
}
);
// return the contact point that has the biggest penetration depth
return l
},
// Detect collision between a circle and a rectangle
// params: circle, rect
cr=(circle,rect)=>{
// try to detect a collision between the circle and the rectangle's edges
// if no edge collision is found, test against the rectangle's corners
// return the resulting contact information (if any)
return cre(circle,rect)||crc(circle,rect);
},
// Detect a collision between a circle and a rectangle's edges
// params: circle, rectangle
cre=(circle,rect,t,c,i=null,v=null,o=0,z,u)=>{
// for each edge
for(;o<4;o++)
// create a vector z from first vertex of edge to the center of the circle
z=s(circle.center,rect.vertices[o]),
// create a vector t from first vertex to the second
t=s(rect.vertices[(o+1)%4],rect.vertices[o]),
// project z on t
c=d(z,n(t)),
// project z on the edge's normal
// if the circle's center is within the edge's bounds and inside the rectangle, save the normal in v and the vertex in i
d(z,rect.normals[o])>=0&&c>0&&c<l(t)&&(v=rect.normals[o],i=rect.vertices[o]);
// no collision if v or i is null
if(v===null||i===null)return null;
// compute distance between edge and circle's center
u=d(v,s(circle.center,i));
// return null (if no collision) or a manifold
return u-circle.size1<0
?{
depth:-(u-circle.size1),
normal:S(v,-1),
contactPoint:A(circle.center,S(v,-circle.size1))
}
:null
},
// Detect a collision between a circle and a rectangle's vertices
// params: circle, rectangle
crc=(circle,rect,t,c=0)=>{
for(;c<4;c++)
if(t=s(rect.vertices[c],circle.center),l(t)<circle.size1)
return{
depth:circle.size1-l(t),
normal:n(t),
contactPoint:rect.vertices[c]
};
return null
}Functions related to collision resolutions:
All the variables are factorized or put in the parameters list.
A "scalar cross" helper function is added.
Minified size: 1177b → 959b.
// Correct positioning
// Move shapes away from each other according to a collision manifold and proportionally to their inverse mass
// params: shape1, shape2, manifold
oc=(shape1,shape2,manifold,v)=>{
// compute total correction amount
v=S(manifold.normal,manifold.depth/(shape1.invMass+shape2.invMass));
// tanslate shapes (if they're not fixed)
shape1.invMass>0&&ts(shape1,S(v,-shape1.invMass)),
shape2.invMass>0&&ts(shape2,S(v,shape2.invMass))
},
// "Scalar cross" helper function
// performs a scalar cross between an angular velocity and penetration vector
// params: shape, penetration
sc=(shape,penetration)=>V(-shape.angularVelocity*penetration.y,shape.angularVelocity*penetration.x),
// Resolve collision
// params: shape1, shape2, manifold
rc=(shape1,shape2,manifold,a,o,v,y,m,u,M,g,f,h,x,F,P,b,j,p,q)=>{
// skip if both shapes are fixed
shape1.invMass===0&&shape2.invMass===0||(
// if the objects are already moving apart from each other, return
// else, compute relative velocity (v: linear and a: rotational)
(y=d(v=s(A(shape2.velocity,sc(shape2,o=s(manifold.contactPoint,shape2.center))),A(shape1.velocity,sc(shape1,a=s(manifold.contactPoint,shape1.center)))),manifold.normal))>0||(
// Normal impulse:
// total restitution
m=Math.min(shape1.restitution,shape2.restitution),
// "lever arm" cross product
u=C(a,manifold.normal),
M=C(o,manifold.normal),
// compute scalar impulse magnitude F
F=S(manifold.normal,x=(-(1+m)*y)/((g=shape1.invMass+shape2.invMass)+(u*u*(f=shape1.invInertia)+M*M*(h=shape2.invInertia)))),
// apply linear impulses (in opposite directions)
shape1.velocity=s(shape1.velocity,S(F,shape1.invMass)),
shape2.velocity=A(shape2.velocity,S(F,shape2.invMass)),
// apply rotational impulses (also opposite)
shape1.angularVelocity+=-u*x*f,
shape2.angularVelocity+=M*x*h,
// Frictional impulse:
// compute reverse tangent direction
P=S(s(v,S(manifold.normal,d(v,manifold.normal))),-1),
// compute frictional impulse and don't let it exceed normal impulse
(p=(-(1+m)*d(v,P)*Math.min(shape1.friction,shape2.friction))/(g+((b=C(a,P))*b*f+(j=C(o,P))*j*h)))>x&&(p=x),
// apply linear and rotational impulses
shape1.velocity=s(shape1.velocity,S(q=S(P,p),shape1.invMass)),
shape2.velocity=A(shape2.velocity,S(q,shape2.invMass)),
shape1.angularVelocity+=-b*p*f,
shape2.angularVelocity+=j*p*h
)
)
}Debug functions and mouse interactions are barely simplified (they will not be present in the final release).
Minified size: 781b → 435b.
// Debug: Draw a point
dp=(center,color= "#888")=>(
c.beginPath(),
c.fillStyle=color,
c.arc(center.x,center.y,5,0,7),
c.fill(),
c.closePath()
),
// Debug: draw a line
dl=(start,end,color="#888")=>(
c.beginPath(),
c.strokeStyle=color,
c.moveTo(start.x,start.y),
c.lineTo(end.x,end.y),
c.stroke(),
c.closePath()
),
// Mouse interactions
mi=(r,a,e,n,o)=>{
if(p)
for(r=0;r<H.length;r++)pi(m,H[r])&&0==sr&&(
sr=H[r],
sp=V(m.x,m.y),
e=s(m,H[r].center),
sa=anchor(e,H[r])
);
else 0!=sr&&(
sr.anchorPoints.pop(),
sr=0
),
sa=0,
sp=0;
sr&&sp&&(
n=sr.anchorPoints[sa],
o=s(m,n),
af(n,sr,S(o,.01))
)
}The update function is a bit simpler.
Minified size: 919b → 618b.
// Update the physics engine
up=(e,r,c,t,o,j=0,i)=>{
// reset manifolds list
M=[];
// consider all distinct pairs of shapes
for(;j<H.length;j++){
// r: shape1 (index j from 0 to H.length)
r=H[j];
// add (gravity * mass) to shape1
r.forceAccumulator=A(r.forceAccumulator,S(G,r.mass));
for(i=j;i<H.length;i++){
// c: shape2 (index i from j to H.length)
c=H[i],
// ignore self-collisions, pairs of fixed shapes and collisions in fixed/hinge joints
j===i||r.invMass===0&&c.invMass===0||r.noCollision.includes(i)||
(
// reset manifold
e=null,
// circle-circle collision
r.type==="circle"&&c.type==="circle"
?(
// vector between circles centers
t=s(c.center,r.center),
// if distance between centers is smaller than sum of radii: collision
(o=l(t))<r.size1+c.size1&&(
// create manifold
e={
depth:r.size1+c.size1-o,
normal:n(t),
contactPoint:A(r.center,S(n(t),r.size1))
}
)
)
// rectangle-rectangle-rectangle collision
:r.type==="rectangle"&&c.type==="rectangle"
?e=rr(r,c)
// rectangle-circle collision
:r.type==="rectangle"&&c.type==="circle"
// inverse r and c and check circle-rectangle collision
?(t=r,r=c,c=t,e=cr(r,c))
// circle-rectangle collision
:r.type==="circle"&&c.type==="rectangle"&&(e=cr(r,c)),
// if a manifold is present: there's a collision
e&&(
// correct positioning
pc(r,c,e),
// resolve collision
rc(r,c,e),
// add manifold to manifolds list (debug only)
M.push(e)
)
);
}
}
// integrate all shapes
for(j of H)si(j);
// handle mouse interactions
mi();
// handle joints
hj();
}The draw function is barely touched (it will not be part of the final release).
Minified size: 705b → 655b.
// Render the scene
dr=(e,r)=>{
for(e of(a.width^=0,H))
for(r of(
c.save(),
c.beginPath(),
"circle"===e.type
?(
c.fillStyle=e.color,
c.translate(e.center.x,e.center.y),
c.rotate(e.angle),
c.arc(0,0,e.size1,0,7),
c.lineTo(0,0),
c.closePath(),
c.fill(),
c.stroke()
):"rectangle"===e.type&&(
c.fillStyle=e.color,
c.moveTo(e.vertices[0].x,e.vertices[0].y),c.lineTo(e.vertices[1].x,e.vertices[1].y),c.lineTo(e.vertices[2].x,e.vertices[2].y),c.lineTo(e.vertices[3].x,e.vertices[3].y),c.closePath(),
c.fill(),
c.stroke()
),
c.restore(),
e.anchorPoints))
dp(r,"green");
for(e of M)
dp(e.contactPoint,"#04F");
for(e of J)
dl(e.rigiA.anchorPoints[e.anchorA],e.rigiB.anchorPoints[e.anchorB],"orange")
};Joints and main loop are also quiclky minified for now. They will be optimized later.
Joints constructors avoid using a temp var for the return, as "J.push()" returns the last item pushed.
Minified size: 4294b → 3794b
// Force joint
// params: rigiA, anchorA, rigiB, anchorB, strength
forceJoint=(rigiA,anchorA,rigiB,anchorB,strength)=>{
return J.push({
type:"force",
rigiA,
anchorA,
rigiB,
anchorB,
strength
})
},
// Spring joint
// params: rigiA, anchorA, rigiB, anchorB, stiffness, restLength
springJoint=(rigiA,anchorA,rigiB,anchorB,stiffness,restLength)=>{
return J.push({
type:"spring",
rigiA,
anchorA,
rigiB,
anchorB,
stiffness,
restLength
});
},
// Reverse force joint
// params: rigiA, anchorA, rigiB, anchorB, strength, maxEffectDistance
reverseForceJoint=(rigiA,anchorA,rigiB,anchorB, strength, maxEffectDistance)=>{
return J.push({
type:"reverseForce",
rigiA,
anchorA,
rigiB,
anchorB,
strength,
maxEffectDistance
})
},
// Fixed joint
// params: rigiA, anchorA, rigiB, anchorB, iterations
fixedJoint=(rigiA,anchorA,rigiB,anchorB,iterations=20)=>{
return rigiA.noCollision.push(H.indexOf(rigiB)),rigiB.noCollision.push(H.indexOf(rigiA)),J.push(e={
type:"fixed",
rigiA,
anchorA,
rigiB,
anchorB,
iterations,
rigiABounce:rigiA.restitution,
rigiBBounce:rigiB.restitution,
rigiAFriction:rigiA.friction,
rigiBFriction:rigiB.friction,
initialLength:l(s(rigiA.anchorPoints[anchorA],rigiB.anchorPoints[anchorB])),
relativeAngle:rigiB.angle-rigiA.angle
})
},
// Hinge joint
// params: rigiA, anchorA, rigiB, anchorB, iterations
hingeJoint=(rigiA,anchorA,rigiB,anchorB,iterations=20)=>{
return rigiA.noCollision.push(H.indexOf(rigiB)),rigiB.noCollision.push(H.indexOf(rigiA)),J.push(e={
type:"hinge",
rigiA,
anchorA,
rigiB,
anchorB,
iterations,
rigiABounce:rigiA.restitution,
rigiBBounce:rigiB.restitution,
rigiAFriction:rigiA.friction,
rigiBFriction:rigiB.friction,
initialLength:l(s(rigiA.anchorPoints[anchorA],rigiB.anchorPoints[anchorB]))
})
},
// Enable/disable friction and restitution in fixed/hinge joints
setMaterialZero=i=>{
i.rigiA.restitution=i.rigiA.friction=i.rigiB.restitution=i.rigiB.friction=0
},
restoreMaterial=i=>{
i.rigiA.restitution=i.rigiABounce,
i.rigiA.friction=i.rigiAFriction,
i.rigiB.restitution=i.rigiBBounce,
i.rigiB.friction=i.rigiBFriction
},
// Joint handler
hj=(i,r,g,t,e,a,o,h,A,B,c,f,p,v,M,m,L,d,y)=>{
for(m=0;m<J.length;m++){
r=0==(i=J[m]).rigiA.invMass||0==i.rigiB.invMass?1:.5,g=i.rigiA.anchorPoints[i.anchorA],
t=i.rigiB.anchorPoints[i.anchorB],
e=s(t,g),
a=l(e);
if("force"==i.type)
af(t,i.rigiA,S(e,i.strength/2)),
af(g,i.rigiB,S(e,-i.strength/2));
else if("spring"==i.type)
o=(a-i.restLength)*i.restLength*i.stiffness*r,h=S(n(e),o),
0!=i.rigiA.invMass&&af(g,i.rigiA,h),
0!=i.rigiB.invMass&&af(t,i.rigiB,S(h,-1));
else if("reverseForce"==i.type)
o=Math.max(0,i.maxEffectDistance-a),
0!=i.rigiA.invMass&&af(t,i.rigiA,S(n(e),-o*i.strength*r)),
0!=i.rigiB.invMass&&af(g,i.rigiB,S(n(e),o*i.strength*r));
else if("fixed"==i.type){
setMaterialZero(i),
d=s(t,g),(L=i.rigiA.invMass+i.rigiB.invMass)>0&&(v=S(d,i.rigiA.invMass/L),
M=S(d,i.rigiB.invMass/L),
ts(i.rigiA,v),
ts(i.rigiB,S(M,-1)));
for(y=0;y<i.iterations&&(e=s(t,g),!((a=l(e))<1e-5));y++)
A={
depth:0,
normal:n(e),
contactPoint:t,
rigiA:i.rigiB,
rigiB:i.rigiA
},
a>i.initialLength?A.depth=a-i.initialLength:(
A.depth=i.initialLength-a,
A.normal=S(A.normal,-1)
),
pc(i.rigiA,i.rigiB,A),
rc(i.rigiA,i.rigiB,A);
B=i.rigiB.angle-i.rigiA.angle-.01,
c=i.relativeAngle-B,
f=1,
i.rigiA.angle-=c*f*.5,
i.rigiB.angle+=c*f*.5;
for(y=0;y<i.iterations&&(e=s(t,g),!((a=l(e))<1e-5));y++)
A={
depth:0,
normal:n(e),
contactPoint:t,
rigiA:i.rigiA,
rigiB:i.rigiB
},
a>i.initialLength?A.depth=a-i.initialLength:(
A.depth=i.initialLength-a,
A.normal=S(A.normal,-1)
),
pc(i.rigiB,i.rigiA,A),
rc(i.rigiB,i.rigiA,A);
B=i.rigiA.angle-i.rigiB.angle,
c=i.relativeAngle-B,
f=1,
i.rigiA.angle+=c*f*.5,
i.rigiB.angle-=c*f*.5,
p=.5*(i.rigiA.angularVelocity+i.rigiB.angularVelocity),
i.rigiA.angularVelocity=p,
i.rigiB.angularVelocity=p,
restoreMaterial(i)
}
else if("hinge"==i.type){
setMaterialZero(i);
d=s(t,g);
(L=i.rigiA.invMass+i.rigiB.invMass)>0&&(
v=S(d,i.rigiA.invMass/L),
M=S(d,i.rigiB.invMass/L),
ts(i.rigiA,v),
ts(i.rigiB,S(M,-1))
);
for(y=0;y<i.iterations&&(e=s(t,g),!((a=l(e))<1e-5));y++)
A={
depth:0,
normal:n(e),
contactPoint:t,
rigiA:i.rigiB,
rigiB:i.rigiA
},
a>i.initialLength?A.depth=a-i.initialLength:(
A.depth=i.initialLength-a,
A.normal=S(A.normal,-1)
),
pc(i.rigiA,i.rigiB,A),
rc(i.rigiA,i.rigiB,A);
for(y=0;y<i.iterations&&(e=s(t,g),!((a=l(e))<1e-5));y++)
A={
depth:0,
normal:n(e),
contactPoint:t,
rigiA:i.rigiA,
rigiB:i.rigiB
},
a>i.initialLength?A.depth=a-i.initialLength:(
A.depth=i.initialLength-a,
A.normal=S(A.normal,-1)),
pc(i.rigiB,i.rigiA,A),
rc(i.rigiB,i.rigiA,A);
restoreMaterial(i)
}
}
};
// Main loop
setInterval(() => {
up();
dr();
}, 16);So far, the full code without demo went from 12133b to 9252b (minified) and 3537b to 3002b (zipped)
THE PLAYROOM
Before continuing, I coded a little demo with 6 different parts showcasing each joint plus a "stress test" with a lot of shapes that collide with each other.
The performance was good (no slowdowns), but some bugs appeared:
- The stress test never reaches an equilibrium state (the shapes keep mobing and rotating infinitely).
- The stress test shapes tend to interpenetrate a bit instead of pushing each other away.
- The fixed joint isn't stiff enough (the circle slowly falls toward the floor).
With the help of ChatGPT and other 2D physics libraries, I learned how to fix these problems, at least in theory:
- The solver can be run many (usually around 10) times per frame to reduce interpenetrations.
- We can use angular impulses to enforce the fixed joint's relative angle.
- We can also remove rc (resolveCollision) from the fixed joint code to avoid applying too many impulses to the neighbour shapes.
This looks better, but the code is hacky and too verbose.
So, let's try putting all these fixes aside and recoding the "update" and "handle joints" methods cleanly, from scratch, based on all that I've seen so far.
OPTIMIZATION
Let's focus on the stress test first:
To make it more stable with minimal extra code, we can:
- remove pc (positional correction) entirely.
- solve the collisions many times per frame in up (update).
- add a Baumgarte-like bias and clamp the friction in rc (resolve collision).
- pseudo-sleep in si (shape integration): set tiny movement/rotations to zero.
In the update function, a reference to both shapes is stored in each manifold, for simplicity.
An ai (apply impulse, linear and angular) method is also added, because it will be necessary at any different places.
// Apply normal impulse (linear + angular)
ai=(sA, sB, impulseScalar, normal, raCrossN, rbCrossN, doLinear=1, Imp) => {
// linear
if(doLinear){
Imp = S(normal, impulseScalar);
if(sA.invMass !== 0) sA.velocity = s(sA.velocity, S(Imp, sA.invMass));
if(sB.invMass !== 0) sB.velocity = A(sB.velocity, S(Imp, sB.invMass));
}
// angular
sA.angularVelocity -= raCrossN * impulseScalar * sA.invInertia;
sB.angularVelocity += rbCrossN * impulseScalar * sB.invInertia;
},
// Shape integration
si=shape=>{
// skip fixed objects
if(shape.invMass!==0){
// add force accumulator to velocity (proportionally to inverse mass)
shape.velocity=A(shape.velocity,S(shape.forceAccumulator,shape.invMass));
// add velocity to position
ts(shape,shape.velocity);
// damp velocity
shape.velocity=S(shape.velocity,.99);
// zero tiny velocity
if(Math.abs(l(shape.velocity)) < .0001) shape.velocity = V(0,0);
// reset force accumulator
shape.forceAccumulator=V(0,0);
// add torque to angular velocity (proportionally to inverse inertia)
shape.angularVelocity+=shape.torqueAccumulator*shape.invInertia;
// add angular velocity to angle
rs(shape,shape.angularVelocity);
// damp angular velocity
shape.angularVelocity*=.99;
// zero tiny rotation
if(Math.abs(shape.angularVelocity) < .0001 || Math.abs(l(shape.velocity)) < .0001) shape.angularVelocity = 0;
// reset torque accumulator
shape.torqueAccumulator=0;
}
},
// Resolve collision
// params: shape1, shape2, manifold
rc=(manifold,shape1,shape2,a,o,v,u,M,B,x,F,P,b,j,m,p,q)=>{
shape1 = manifold.A;
shape2 = manifold.B;
// Movement impulses
// skip if both shapes are fixed
if(shape1.invMass!==0 || shape2.invMass!==0){
// relative velocity at contact point
v = s(
A(
shape2.velocity,
sc(
shape2,
o = s(manifold.contactPoint, shape2.center)
)
),
A(
shape1.velocity,
sc(
shape1,
a = s(manifold.contactPoint, shape1.center)
)
)
);
// effective mass for normal direction
u = C(a,manifold.normal);
M = C(o,manifold.normal);
// compute Baumgarte-like bias from penetration to reduce positional drift
B = manifold.depth * .5;
// normal impulse scalar
x = (-(1 + Math.min(shape1.restitution, shape2.restitution)) * d(v, manifold.normal) + B) / (shape1.invMass + shape2.invMass + u*u*shape1.invInertia + M*M*shape2.invInertia);
// apply impulses
ai(shape1, shape2, x, manifold.normal, u, M);
// friction impulses
// compute tangent
P = S(s(v, S(manifold.normal, d(v, manifold.normal))), -1);
// if zero tangent, skip
if(l(P) > 0) {
// effective mass along tangent
b = C(a, P = n(P));
j = C(o, P);
// friction coefficient
m = Math.min(shape1.friction, shape2.friction);
// desired friction impulse
p = (-d(v, P)) / (shape1.invMass + shape2.invMass + b*b*shape1.invInertia + j*j*shape2.invInertia);
// clamp friction by normal impulse magnitude
if(Math.abs(p) > Math.abs(x) * m) p = Math.sign(p) * Math.abs(x) * m;
// apply impulses
ai(shape1, shape2, p, P, b, j);
}
}
},
// Update the physics engine
up=(i,j,body1,body2,manifold,diff,dist)=>{
// clear manifolds
M = [];
// reset acceleration and apply gravity (F = m * g)
for(j of H){
if(j.invMass !== 0) j.forceAccumulator = S(G, j.mass);
}
// collision detection
for(j=0;j<H.length;j++){
for(i=j+1;i<H.length;i++){
body1 = H[j],
body2 = H[i];
// skip pairs of static bodies and bodies with fixed/hinge joints
if((body1.invMass !== 0 || body2.invMass !== 0) && !body1.noCollision.includes(i)){
// reset manifold
manifold = null;
// circle-circle
if(body1.type=== "circle" && body2.type === "circle"){
diff = s(body2.center, body1.center);
dist = l(diff);
if(dist < body1.size1 + body2.size1){
manifold = {
depth: body1.size1 + body2.size1 - dist,
normal: n(diff),
contactPoint: A(body1.center, S(n(diff), body1.size1)),
A: body1,
B: body2
};
}
}
// rect-rect
else if(body1.type === "rectangle" && body2.type === "rectangle"){
manifold = rr(body1, body2);
}
// rect-circle (circle as first)
else if(body1.type === "rectangle" && body2.type === "circle"){
manifold = cr(body2, body1);
}
// circle-rect
else { //if(body1.type === "circle" && body2.type === "rectangle"){
manifold = cr(body1, body2);
}
// add manifold to list
if(manifold) M.push(manifold);
}
}
}
// resolve contact impulses and joint impulses multiple times
for(i = 20; i--;){
// resolve contacts
for(j of M){
rc(j);
}
// resolve joints as contact-like constraints
hj();
}
// integrate shapes
for(j of H) si(j);
},It's not perfect, but it's more stable than ever and there are almost no residual interpenetrations.
For the joints, we can use a unified constructor function instead of five, and rewrite the hj (handle joints) function like this:
solve the joints with impulses, many times per frame.
after each resolution, apply a slight positional correction to help the anchors stay attached for hinge and fixed joints.
get rid of material enabling/disabling code and the D (dist) Vec2 function.
// Joints
// type: force/spring/repulse/hinge/fixed
// length: restLength (spring), minDistance (repulse)
joint=(type,rigiA,anchorA,rigiB,anchorB,strength,length,relativeAngle)=>{
// hinge/fixed: disable collisions
if(type === "hinge" || type === "fixed"){
rigiA.noCollision.push(H.indexOf(rigiB));
rigiB.noCollision.push(H.indexOf(rigiA));
relativeAngle=rigiB.angle-rigiA.angle;
}
return J.push({
type,
rigiA,
anchorA,
rigiB,
anchorB,
strength,
length,
relativeAngle
});
},
// Handle joints
hj = () => {
var baumgarte = 0.4, // rigidity (0.1–0.4)
softness = 0.01, // stabilization
j, sA, B, Apos, Bpos, ra, rb, dpos, dist, normal, raCrossN, rbCrossN, invMassSum, err, angMass, totalInvMass;
for(j of J){
sA = j.rigiA;
B = j.rigiB;
// world anchors
Apos = sA.anchorPoints[j.anchorA];
Bpos = B.anchorPoints[j.anchorB];
// relative vectors
ra = s(Apos, sA.center);
rb = s(Bpos, B.center);
// separation
dpos = s(Bpos, Apos);
dist = l(dpos);
normal = dist > 0 ? n(dpos) : V(1,0);
// effective mass
raCrossN = C(ra, normal);
rbCrossN = C(rb, normal);
invMassSum = sA.invMass + B.invMass + raCrossN * raCrossN * sA.invInertia + rbCrossN * rbCrossN * B.invInertia + softness;
if(invMassSum !== 0){
// force joint
if(j.type === "force"){
ai(sA, B, (-(j.strength * dist) / 10000), normal, raCrossN, rbCrossN);
}
// spring joint
else if(j.type === "spring"){
ai(sA, B, ((-(j.strength * (dist - j.length)) / 1000) / invMassSum), normal, raCrossN, rbCrossN);
}
// repulsion joint
else if(j.type === "repulse"){
ai(sA, B, ((j.strength * Math.max(0, j.length - dist)) / 10000), normal, raCrossN, rbCrossN);
}
// hinge / fixed
else {
// linear impulses
ai(sA, B, (-(d(s(A(B.velocity, sc(B, rb)), A(sA.velocity, sc(sA, ra))), normal)) + (-(baumgarte * dist))) / invMassSum, normal, raCrossN, rbCrossN)
// angular correction (fixed only)
if(j.type === "fixed"){
err = (B.angle - sA.angle) - (j.relativeAngle);
angMass = sA.invInertia + B.invInertia;
if(angMass > 0){
ai(sA, B, (-(B.angularVelocity - sA.angularVelocity) + (-(baumgarte * err)) ) / angMass, 0, 1, 1, 0);
}
}
// position correction (anchors superposed)
if(dist > 0){
totalInvMass = sA.invMass + B.invMass;
if(sA.invMass !== 0) ts(sA, S(dpos, (sA.invMass / totalInvMass)));
if(B.invMass !== 0) ts(B, S(dpos, -(B.invMass / totalInvMass)));
}
}
}
}
},
// Demo
// Grid
shape("rectangle", V(400, 20), 780, 20, 0, .5, .5);
shape("rectangle", V(400, 300), 780, 20, 0, .5, .5);
shape("rectangle", V(400, 580), 780, 20, 0, .5, .5);
shape("rectangle", V(20, 300), 20, 580, 0, .5, .5);
shape("rectangle", V(280, 300), 20, 580, 0, .5, .5);
shape("rectangle", V(540, 300), 20, 580, 0, .5, .5);
shape("rectangle", V(780, 300), 20, 580, 0, .5, .5);
// Stress test
for(i=35;i--;){
shape("circle", V(65 - i/2 + (i % 8) * 25, 55+ (i / 8) * 40), 10, 15, 1, .5, .5);
shape("rectangle", V(50 + i/2 + (i % 8) * 25, 35+ (i / 8) * 40), 20, 15, 1, .5, .5, );
}
// Force joint
r1 = shape("rectangle", V(400, 80), 90, 50, 0, .5, .5);
a1 = anchor(V(20,15), r1);
c1 = shape("circle", V(450, 250), 30, 30, .5);
a2 = anchor(V(-20,10), c1);
j1 = joint("force", r1, a1, c1, a2, .95);
// Spring joint
r1 = shape("rectangle", V(630, 80), 90, 50, 0, .5, .5);
a1 = anchor(V(20,15), r1);
c1 = shape("circle", V(590, 250), 30, 30, 1);
a2 = anchor(V(0,-10), c1);
j2 = joint("spring", r1, a1, c1, a2, .2, 80);
// repulse force joint
for(i=10;i--;){
shape("circle", V(180+Math.random() * 30, 520+Math.random() * 20), Math.random()*5+5, 10, 10, .5, .5);
}
r1 = shape("rectangle", V(100, 520), 90, 50, 0, .5, .5);
a1 = anchor(V(0,-25), r1);
c1 = shape("circle", V(120, 480), 30, 0, 1);
a2 = anchor(V(-20,0), c1);
j1 =joint("repulse", r1, a1, c1, a2, .2, 200);
// Fixed joint
for(i=20;i--;){
shape("circle", V(300+Math.random() * (780/3 - 50), 520+Math.random() * 20), Math.random()*5+5, 10,10, .5, .5);
}
r1 = shape("rectangle", V(400, 420), 90, 50, 10, .5, .5);
a1 = anchor(V(0,-15), r1);
c1 = shape("circle", V(400, 400), 30, 30, 10);
a2 = anchor(V(0,20), c1);
j4 = joint("fixed", r1, a1, c1, a2);
// Hinge joint
r1 = shape("rectangle", V(630, 460), 90, 50, 0, .5, .5);
a1 = anchor(V(20,15), r1);
c1 = shape("circle", V(665, 465), 30, 30, 100);
a2 = anchor(V(-20,10), c1);
j4 = joint("hinge", r1, a1, c1, a2);With this rewrite (made with a lot of trial and error), all the joints behave correctly: no wobble, no shaking, no exaggerated collisions with the other shapes in the scene!
In terms of size, we are also very good: 7609b minified, 2734b minified !
Here's a new demo testing every possible interaction between joints, mobile and immobile shapes, and multi-jointed shapes:
// Grid
shape("rectangle", V(400, 20), 780, 20, 0, .5, .5);
shape("rectangle", V(280, 300), 500, 20, 0, .5, .5);
shape("rectangle", V(400, 580), 780, 20, 0, .5, .5);
shape("rectangle", V(20, 300), 20, 580, 0, .5, .5);
shape("rectangle", V(280, 300), 20, 580, 0, .5, .5);
shape("rectangle", V(540, 300), 20, 580, 0, .5, .5);
shape("rectangle", V(780, 300), 20, 580, 0, .5, .5);
// Hinge
s1 = shape("rectangle", V(140, 90), 90, 50, 100, .5, .5);
a1 = anchor(V(20,15), s1);
s2c = shape("circle", V(135, 90), 30, 30, 0);
a2 = anchor(V(-20,10), s2c);
j1 = joint("hinge", s1, a1, s2c, a2);
s1 = shape("rectangle", V(150, 270), 20, 50, 0, .5, .5);
a1 = anchor(V(0,-20), s1);
s2 = shape("rectangle", V(150, 240), 160, 20, 100, .5, .5);
a2 = anchor(V(0,0), s2);
j1 = joint("hinge", s1, a1, s2, a2);
s1 = shape("circle", V(170, 150), 20, 20, 10, .5, .5);
a1 = anchor(V(0,-15), s1);
s2 = shape("circle", V(165, 140), 10, 10, 10, .5, .5);
a2 = anchor(V(10,0), s2);
j1 = joint("hinge", s1, a1, s2, a2);
// Multi hinge
s1b = shape("rectangle", V(410, 70), 200, 30, 0, .5, .5);
a1a = anchor(V(-60,10), s1b);
a1b = anchor(V(70,10), s1b);
s2 = shape("circle", V(390, 90), 30, 30, 10, .5, .5);
a2a = anchor(V(20,-20),s2);
a2b = anchor(V(-20,20),s2);
s3 = shape("rectangle", V(450, 110), 30, 60, 10, .5, .5);
a3a = anchor(V(10,-20),s3);
a3b = anchor(V(-10,20),s3);
j1 = joint("hinge", s1b, a1a, s2, a2a);
j2 = joint("hinge", s1b, a1b, s3, a3a);
s6 = shape("circle", V(400, 200), 50, 50, 10, .5, .5);
s4 = shape("rectangle", V(370, 150), 30, 100, 10, .5, .5);
a4a = anchor(V(0,-40),s4);
a4b = anchor(V(0,40),s4);
s5 = shape("rectangle", V(470, 150), 30, 100, 10, .5, .5);
a5a = anchor(V(0,-40),s5);
a5b = anchor(V(0,40),s5);
j3 = joint("hinge", s2, a2b, s4, a4a);
j4 = joint("hinge", s3, a3b, s5, a5a);
a6a = anchor(V(-40,-0),s6);
a6b = anchor(V(40,0),s6);
j5 = joint("hinge", s6, a6a, s4, a4b);
j6 = joint("hinge", s6, a6b, s5, a5b);
// Fixed
s1 = shape("rectangle", V(140, 90+280), 90, 50, 100, .5, .5);
a1 = anchor(V(20,15), s1);
s2d = shape("circle", V(135, 90+280), 30, 30, 0);
a2 = anchor(V(-20,10), s2d);
j1 = joint("fixed", s1, a1, s2d, a2);
s1 = shape("rectangle", V(150, 270+280), 20, 50, 0, .5, .5);
a1 = anchor(V(0,-20), s1);
s2 = shape("rectangle", V(150, 240+280), 160, 20, 100, .5, .5);
a2 = anchor(V(0,0), s2);
j1 = joint("fixed", s1, a1, s2, a2);
s1 = shape("circle", V(170, 150+280), 20, 20, 10, .5, .5);
a1 = anchor(V(0,-15), s1);
s2 = shape("circle", V(165, 140+280), 10, 10, 10, .5, .5);
a2 = anchor(V(10,0), s2);
j1 = joint("fixed", s1, a1, s2, a2);
// Multi fixed
s1a = shape("rectangle", V(410, 70+280), 200, 30, 0, .5, .5);
a1a = anchor(V(-60,10), s1a);
a1b = anchor(V(70,10), s1a);
s2 = shape("circle", V(390, 90+280), 30, 30, 10, .5, .5);
a2a = anchor(V(20,-20),s2);
a2b = anchor(V(-20,20),s2);
s3 = shape("rectangle", V(450, 110+280), 30, 60, 10, .5, .5);
a3a = anchor(V(10,-20),s3);
a3b = anchor(V(-10,20),s3);
j1 = joint("fixed", s1a, a1a, s2, a2a);
j2 = joint("fixed", s1a, a1b, s3, a3a);
s6 = shape("circle", V(400, 200+280), 50, 50, 10, .5, .5);
s4 = shape("rectangle", V(370, 150+280), 30, 100, 10, .5, .5);
a4a = anchor(V(0,-40),s4);
a4b = anchor(V(0,40),s4);
s5 = shape("rectangle", V(470, 150+280), 30, 100, 10, .5, .5);
a5a = anchor(V(0,-40),s5);
a5b = anchor(V(0,40),s5);
j3 = joint("fixed", s2, a2b, s4, a4a);
j4 = joint("fixed", s3, a3b, s5, a5a);
a6a = anchor(V(-40,-0),s6);
a6b = anchor(V(40,0),s6);
j5 = joint("fixed", s6, a6a, s4, a4b);
j6 = joint("fixed", s6, a6b, s5, a5b);
// Hinge + fixed
s1p = shape("rectangle", V(650, 70), 100, 30, 0, .5, .5);
a1 = anchor(V(0,15), s1p);
s2 = shape("circle", V(650, 90), 30, 30, 10, .5, .5);
s3 = shape("rectangle", V(650, 110), 50, 50, 10, .5, .5);
s4 = shape("rectangle", V(590, 180), 100, 50, 10, .5, .5);
s5 = shape("circle", V(650, 270), 30, 30, 10, .5, .5);
a2a = anchor(V(20,-20),s2);
a2b = anchor(V(0,20),s2);
a3a = anchor(V(20,-20),s3);
a3b = anchor(V(20,20),s3);
a4a = anchor(V(40,-20),s4);
a4b = anchor(V(-40,20),s4);
a5a = anchor(V(-20,-20),s5);
j1 = joint("hinge", s1p, a1, s2, a2a);
j2 = joint("fixed", s2, a2b, s3, a3a);
j3 = joint("hinge", s3, a3b, s4, a4a);
j4 = joint("fixed", s4, a4b, s5, a5a);
Good enough!
GOLFING MY ENGINE
Phase 2: final obfuscation and API
Now that the engine works as I expected, I can finish golfing it by merging functions, removing useless code, renaming long variables & attributes, and adding / optimizing a ton of tiny things.
Functions merged in run(): N (Vec2 normal), si (shape integration), rr (rectangle-rectangle collision detection), cp (contact point) fs (find a support point), cr (circle vs rectangle), cre (circle vs rectangle edges), crc (circle vs rectangle corners), rc (resolve collision), dp (draw point), dl (draw line), hj (handle joints), in (integrate)...
Stuff put in the global scope: G (gravity), O, E, R (stability parameters), H, J, M (shapes, joints, manifolds)...
Stuff removed: normalscale (in circle-rectangle detection), force joints (just a special case of spring joint), ...
Stuff renamed / modified:
- null → 0
- a === 1 → a, a !== 0 → a, ...
- the API (shape(), anchor(), joint(), run()).
- No global leak for the other methods (IIFE).
- shapes types and joints types are now number constants
- all attributes in shape, joint, manifold, contact point are now one letter long.
- Multi-purpose variables in run()
- Better for-oops everywhere
Features added: shapes initial angle, velocity, angularVelocity, custom gravity, custom color (or any other data)
Minified size: 1448 bytes gzipped (1152b without joints)
// API
// -----
// - shape(type, center, mass, width, height, {f: friction, r:restitution, a: angle, v: velocity, a: angularVelocity, g: gravity, d: customData)
// - anchor(shape, position)
// - joint(type, shape1, anchor1, shape2, anchor2, strength, length)
// - run(): run simulation
// Globals
// ---------
// Constants
G = [0,.1]; // Gravity
O = .4; // Shapes overlap correction
E = .01; // Fixed joints elasticity
R = 20; // Resolutions per frame
// Arrays
H = []; // shapes (circles, rectangles)
J = []; // joints (spring, repulsive, hinge, fixed)
M = []; // manifolds (collision info)
// Shapes types
RECTANGLE = 0;
CIRCLE = 1;
// Joints types
SPRING = 0;
REPULSIVE = 1;
HINGE = 2;
FIXED = 3;
((n=x=>S(x,1/l(x)),l=x=>d(x,x)**.5,d=(x,y)=>x[0]*y[0]+x[1]*y[1],p=(x,y)=>[x[0]+y[0],x[1]+y[1]],s=(x,y)=>p(x,S(y,-1)),S=(x,y)=>[x[0]*y,x[1]*y],C=(x,y)=>x[0]*y[1]-x[1]*y[0],r=(x,y,l)=>[(x[0]-y[0])*Math.cos(l)-(x[1]-y[1])*Math.sin(l)+y[0],(x[0]-y[0])*Math.sin(l)+(x[1]-y[1])*Math.cos(l)+y[1]],x=(x,y)=>[-x.A*y[1],x.A*y[0]],X=(c,f,n,i=4)=>{if(c.c=p(c.c,f),!c.t)for(;i--;)c.n[i]=r(c.n[i],[0,0],n),c.V[i]=r(p(c.V[i],f),c.c,n);for(i in c.p)c.p[i]=r(p(c.p[i],f),c.c,n)},I=(c,t,l,e,a,n,r=1,o)=>{r&&(o=S(e,l),c.v=s(c.v,S(o,c.M)),t.v=p(t.v,S(o,t.M))),c.A-=a*l*c.I,t.A+=n*l*t.I})=>{shape=(t,c,m=1,w=9,h=9,g,n=t?m*w*w/2:m*(w*w+h*h)/12,s={t,m,w,h,c:[0,0],f:.5,r:.5,a:0,v:[0,0],A:0,g:G,F:[0,0],T:0,p:[],N:[],n:[[0,-1],[1,0],[0,1],[-1,0]],M:m?1/m:0,I:n?1/n:0,V:[[-w/2,-h/2],[w/2,-h/2],[w/2,h/2],[-w/2,h/2]],e:H.length,...g})=>(X(s,c,s.a),H.push(s),s),anchor=(t,c)=>(t.p.push(p(c,t.c)),t.p.length-1),joint=(t,A,a,B,b,s,l)=>{if(t>1){A.N.push(B.e);B.N.push(A.e);l=B.a-A.a}J.push({t,A,a,B,b,s,l})},run=(a,f,t,c,e,h,o,r,A,v,w,i,V,b,B,m,g)=>{for(M=[],f=H.length;f--;)for(a=f-1;a>=0;a--)if(c=H[f],e=H[a],c.F=S(c.g,c.m),c.M+e.M&&!c.N.includes(a)){if(h=0,c.t&&e.t)o=s(e.c,c.c),(r=l(o))=0&&w>0&&wA&&(A=w,v={v:e.V[i],d:w});v||(h=0),h&&v.d0&&(b=C(V,w=n(w)),B=C(i,w),m=Math.min(c.f,e.f),g=-d(h,w)/(c.M+e.M+b*b*c.I+B*B*e.I),Math.abs(g)>Math.abs(v)*m&&(g=Math.sign(g)*Math.abs(v)*m),I(c,e,g,w,b,B));for(t of J)c=t.A,e=t.B,h=c.p[t.a],o=e.p[t.b],v=s(h,c.c),w=s(o,e.c),A=s(o,h),i=(r=l(A))>0?n(A):[1,0],V=C(v,i),b=C(w,i),(B=c.M+e.M+V*V*c.I+b*b*e.I+E)&&(t.t?t.t<2?I(c,e,t.s*Math.max(0,t.l-r)/1e4,i,V,b):(I(c,e,(-d(s(p(e.v,x(e,w)),p(c.v,x(c,v))),i)+-O*r)/B,i,V,b),t.t>2&&(m=e.a-c.a-t.l,(g=c.I+e.I)&&I(c,e,(-(e.A-c.A)+-O*m)/g,0,1,1,0)),r>0&&(B=c.M+e.M,X(c,S(A,c.M/B),0),X(e,S(A,-e.M/B),0))):(I(c,e,-t.s*(r-t.l)/1e3/B,i,V,b),I(c,e,-t.s*(r-t.l)/1e3/B,i,V,b)))}for(f of H)f.M&&(f.v=p(f.v,S(f.F,f.M<0?-f.M:f.M)),f.F=[0,0],f.A+=f.T*f.I,f.a+=f.A,X(f,f.v,f.A),f.v=S(f.v,.99),Math.abs(l(f.v))<1e-4&&(f.v=[0,0]),f.A*=.99,Math.abs(f.A)<1e-4&&(f.A=0),f.T=0)}})() Here's my updated demo after 2 weeks of golfing (and 6 weeks of work in total):
New codegolf project! 🚀
— xem 🔵 (@MaximeEuziere) December 5, 2025
- A 2D physics engine in JS featuring springs and joints.
- 1.4kb zipped so far!
- Demo: https://t.co/Ugdy0SunEA
- Source: https://t.co/uvlOTMyLpo
- Making-of: https://t.co/CLO4j3GWcb
- Let's golf? @aemkei @subzey @p01 @KilledByAPixel @Xen_the ... pic.twitter.com/7O6AeC1xqs